
www.
edises
.it
Capitolo 6
Successioni e serie numeriche, calcolo differenziale per funzioni di una variabile
461
Analogamente, se
( )
y f x
=
è una funzione de nita in
X
con valori reali e
x
0
è un punto di accumulazione di
X
. Si dice che il limite sinistro di
f
(
x
) per la
variabile indipendente
x
che tende a
x
0
vale
l
e si scrive
lim ( )
f x l
0
x x
−
→
=
che equi-
vale a dire che:
0
0
0
0 |
( )
]
, [
f x l
x X x
x
e
d
e
d
∀ > ∃ >
− < ∀ ∈ ∩ −
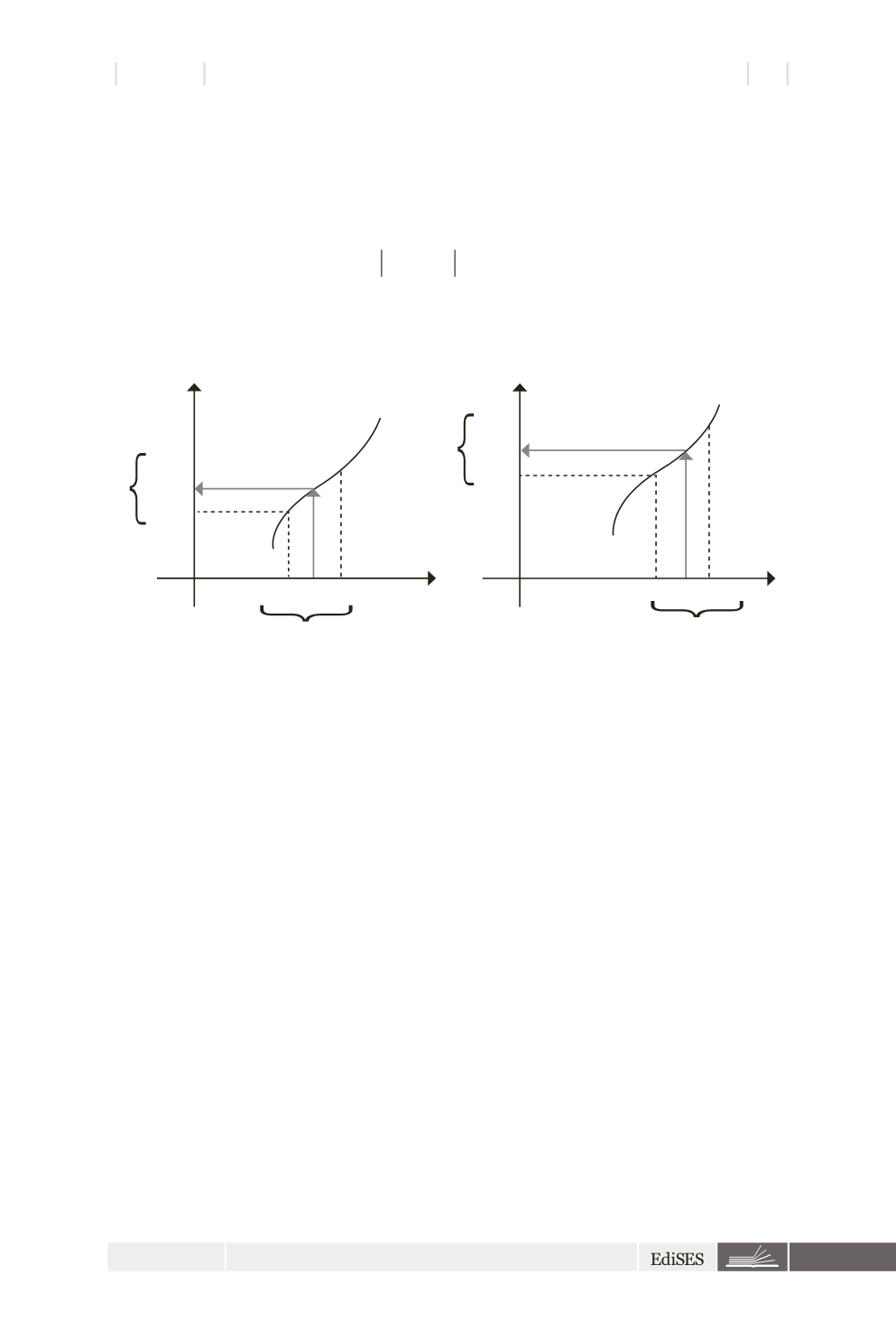
I limiti destro e sinistro sono schematizzati in Figura 5.
Limite sinistro
y
x
f(x)
+ε
f(x)
f(x)-
ε
x
0
-
δ
x
x
0
J
I
-
f(x)
Limite destro
y
x
f(x)
+ε
f(x)
f(x)-
ε
x
0
x
x
0
+δ
J
I
+
f(x)
Figura 5
Si supponga ora che la funzione
( )
y f x
=
diverga positivamente in
x
0
, punto
di accumulazione del suo dominio. Si dice che il limite destro di
f
(
x
) per la
variabile indipendente
x
che tende ad
x
0
vale
+
∞
e si scrive:
0
lim ( )
x x
f x
+
→
= +∞
se in corrispondenza di un numero
δ
> 0 si può determinare un intorno
destro
I
+
di
x
0
, che in particolare è
0 0
] ,
[
I
x x
d
+
= +
tale che, per tutti i valori
x
dell’intorno destro di
x
0
appartenenti al campo di esistenza
X
, è soddisfatta la
disequazione
( )
f x
e
>
ε
dove
ε
è grande a piacere.
In termini simbolici tale asserto si può scrivere come:
0 0
0
0 |
( )
] ,
[
f x
x X x x
e
d
e
d
∀ > ∃ >
> ∀ ∈ ∩ +
Di seguito si riepilogano gli altri casi nei quali per limite destro o sinistro la
funzione diverge positivamente o negativamente.
















