
www.
edises
.it
456
Parte Seconda
Matematica
I
f(x)
ε
f
x
0
-
d
X
x
0
x
0
+
d
y
x
J
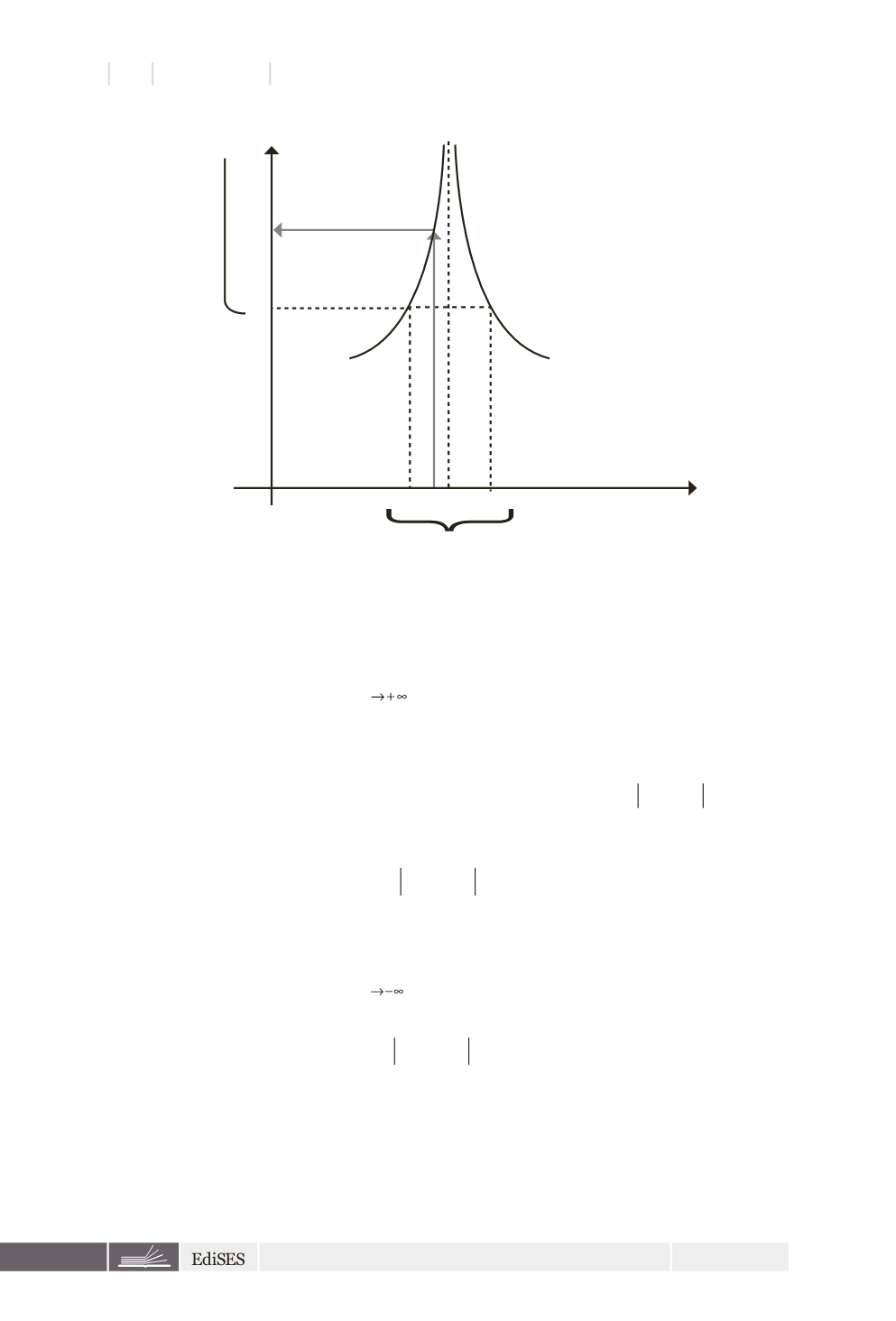
Figura 3
Se, per
x
che tende a +
∞
, il corrispondente valore di
f
(
x
) tende ad un valore
finito
l
, allora si può scrivere
lim ( )
x
f x l
=
.
In tal caso per ogni valore
d
> 0 si può determinare un intorno
I
di +
∞
, che in
particolare è
] ,
[
I
d
= +∞
, tale che, per tutti i valori
x
>
d
, ossia i valori dell’intor-
no di +
∞
appartenenti al campo di esistenza
X
della funzione
f
, si può deter-
minare un
ε
0
e
>
per cui risulta soddisfatta la disequazione
( )
f x l
e
− <
ε
, ossia
( )
l
f x l
e
e
− < < +
.
In termini simbolici tale asserto si può riassumere come:
0
0 |
( )
|
f x l
x X x
e
d
e
d
∀ > ∃ >
− < ∀ ∈ >
L’interpretazione grafica di questo caso è mostrata in Figura 4.
Se, per
x
che tende a -
∞
, il corrispondente valore di
f
(
x
) tende ad un valore
finito
l
, allora si può scrivere
lim
( )
x
f x l
=
.
Tale scrittura equivale a dire che:
0
0 |
( )
|
f x l
x X x
e
d
e
d
∀ > ∃ >
− < ∀ ∈ < −
















