
www.
edises
.it
Capitolo 6
Successioni e serie numeriche, calcolo differenziale per funzioni di una variabile
457
1+
ε
1
f(x)
1-
ε
f
y
x
J
I
X
d
Figura 4
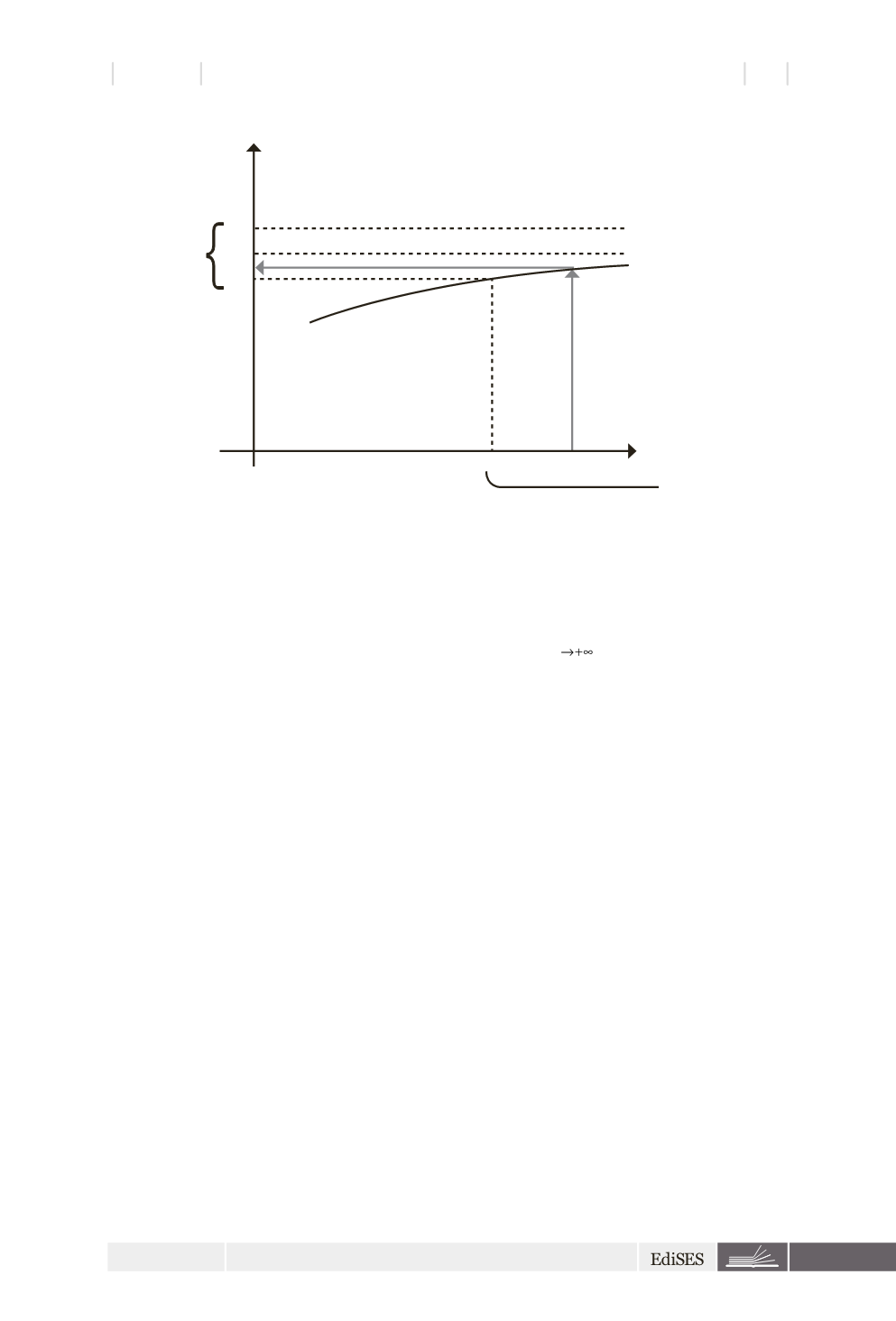
In ultima analisi si presenta il caso in cui per
x
che tende a +
∞
, il corrisponden-
te valore di
f
(
x
) tende a +
∞
. Si può quindi scrivere
lim ( )
x
f x
= +∞
.
Tale scrittura equivale a dire che:
0
0 |
( )
|
f x
x X x
e
d
e
d
∀ > ∃ >
> ∀ ∈ >
Analogamente si può scrivere:
lim ( )
x
f x
→+∞
= −∞
⇔
0
0 |
( )
|
f x
x X x
e
d
e
d
∀ > ∃ >
< − ∀ ∈ >
lim ( )
x
f x
→−∞
= +∞
⇔
0
0 |
( )
|
f x
x X x
e
d
e
d
∀ > ∃ >
> ∀ ∈ < −
lim ( )
x
f x
→−∞
= −∞
⇔
0
0 |
( )
|
f x
x X x
e
d
e
d
∀ > ∃ >
< − ∀ ∈ < −
6.1.4
Verifica del limite
Operare la verifica di un limite significa constatare che l’asserto stabilito dall’E-
quazione 1 è vero. Si riportano degli esempi.
















