
www.
edises
.it
Capitolo 6
Successioni e serie numeriche, calcolo
differenziale per funzioni di una variabile
6.1
Limite di una funzione
6.1.1
Punti di accumulazione
Dato un valore reale
x
ed un sottoinsieme
A
di
R
, si dice che
x
è un
punto
di accumulazione
per
A
se ogni intorno di
x
contiene punti di
A
distinti da
x
. Se un punto non è di accumulazione per un insieme, allora viene detto
isolato
.
Esempio
Si consideri l’intervallo aperto
J
=
]1, 4[
. Il valore
x
= 3 è un punto di accumulazione
per l’intervallo
J
, in quanto, qualsiasi intorno di 3, per quanto piccolo possa essere,
contiene punti di
J
. Difatti il generico intorno di 3 può essere individuato per mezzo
di una quantità
d
> 0, che può essere resa piccola a piacere. L’intorno di 3 può essere
scritto nella forma ]3 –
d
,3 +
d
[. Accade sempre che il generico intorno di 3 abbia
intersezione non nulla con l’intervallo
J
.
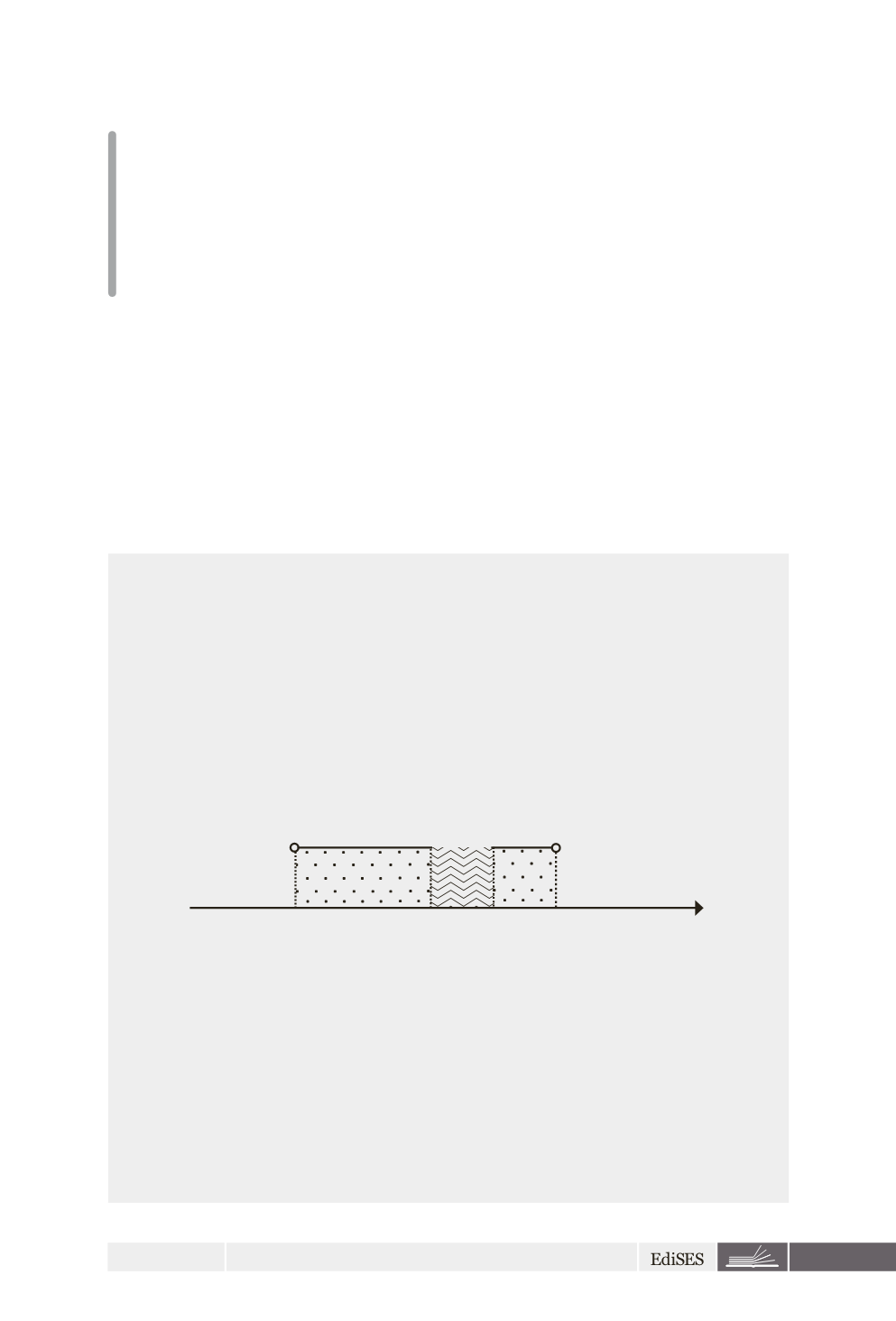
]1, 4[ ]3 ,3 [
d d
∩ − + ≠ ∅
A tal proposito si può confrontare la Figura 1.
R
x
J
3-
d
3 3+
d
4
1
Figura 1
Anche gli estremi dell’intervallo aperto
J
=
]1, 4[
sono punti di accumulazione per
l’intervallo. Ad esempio, qualsiasi intorno del punto
x
= 1 ha sempre intersezione
non nulla con
J
.
]1, 4[ ]1 ,1 [
d d
∩ − + ≠ ∅
Il punto
x
= 5 non è invece un punto di accumulazione per
J
. Infatti basta scegliere
un
d
tale che 0 <
d
< 1 perché l’intorno di 5 costruito come ]5 –
d
, 5 +
d
[ abbia sem-
pre intersezione nulla con
J
.
]1, 4[ ]5 ,5 [
d d
∩ − + = ∅
















