
Parte III - Simulazioni d’esame
542
α
=
°
° −
=
°
° − °
= °
n
360
180
360
180 150
12 .
La somma degli angoli interni di un poligono di 12 lati risulta, infine:
S
a
= (12 – 2) 180° = 1800°.
30)
D.
Indicando con
P
2007
il prezzo del pane a gennaio 2007, il prezzo del
pane a gennaio 2014 risulta:
P
2014
=
P
2007
+ 26%
P
2007
= 1,26 ·
P
2007
.
Il prezzo a gennaio 2008 è, invece:
P
2008
=
P
2007
+ 5%
P
2007
= 1,05 ·
P
2007
.
L’aumento percentuale del prezzo del pane dal 2008 al 2014 risulta, infine:
D
⋅
=
−
⋅
=
⋅
− ⋅
⋅
⋅
=
= ⋅
=
P
P
P P
P
P
P
P
100%
100%
1,26
1,05
1,05
100%
0,21
1,05
100% 20%
2008
2014 2008
2008
2007
2007
2007
31)
B.
La ricerca delle soluzioni dell’equazione
x
3
–
x
2
+ k
= 0, che per il
teorema fondamentale dell’algebra ammette 3 soluzioni in
C
se si conta anche
la molteplicità, può essere ricondotta alla ricerca dei punti di intersezione del
grafico della funzione
y
=
f
(
x
) =
x
3
–
x
2
+
k
con l’asse
x
di equazione
y
=0.
La derivata di
f
è:
f
9
(
x
) = 3
x
2
– 2
x
,
che si annulla per
x
1
=0 e
x
2
= 2/3.
In particolare, nei punti
A
(0,
k
) e
− +
B
k
2
3
,
4
27
il grafico di
f
presenta due
flessi a tangente orizzontale. Per
k
=0 o per
=
k
4
27
l’ordinata di uno dei due
punti a tangente orizzontale è zero: ciò significa che il grafico di
f
è tangente
all’asse
y
e, quindi, la soluzione dell’equazione ha molteplicità 2, essendo pre-
sente una terza radice con molteplicità singola, come si può vedere facilmente
da un grafico qualitativo di
f
che per
x
:
–
`
tende a –
`
e per
x
:
+
`
tende a
+
`
.
32)
C.
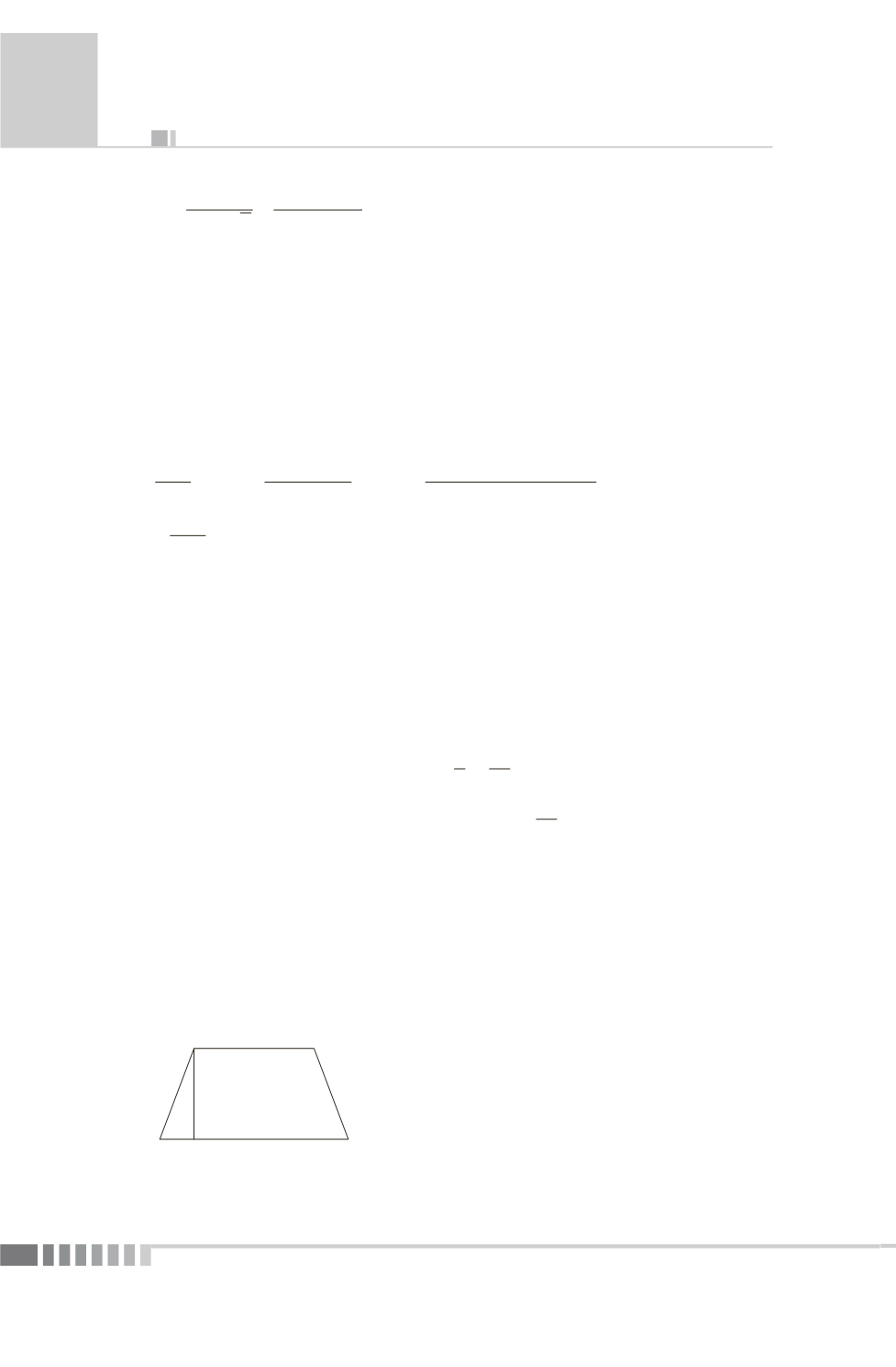
Poiché tre lati sono congruenti, allora il trapezio è isoscele. Si consi-
deri quindi la seguente figura:
D
C
A H
B
















