
Esempi
1) Convertire il numero 10101 nel sistema decimale.
10101 = 1
⋅
2
4
+ 0
⋅
2
3
+ 1
⋅
2
2
+ 0
⋅
2
1
+ 1
⋅
2
0
= 16 + 0 + 4 + 0 + 1 = 21
2) Convertire il numero 1111 nel sistema decimale.
1111 = 1
⋅
2
3
+ 1
⋅
2
2
+ 1
⋅
2
1
+ 1
⋅
2
0
= 8 + 4 + 2 + 1 = 15
Per convertire un numero decimale in uno binario occorre dividere
ripetutamente il numero per 2 e raccogliere i resti ottenuti nelle divi-
sioni. Difatti il resto di una divisione per 2 può essere solo pari a 0
oppure a 1.
Si illustra la procedura nel dettaglio, convertendo il numero decima-
le 72 nel sistema binario.
Si divide 72 per 2, il quoziente è pari a 36 ed il resto è 0. Di seguito si
divide 36 per 2, ottenendo 18 con il resto di 0. Si procede con le divisio-
ni fino a ottenere un quoziente pari ad 1. Si divide tale quoziente unita-
rio per 2 ottenendo un quoziente pari a 0 e un resto pari ad 1 e si termi-
nano le divisioni.
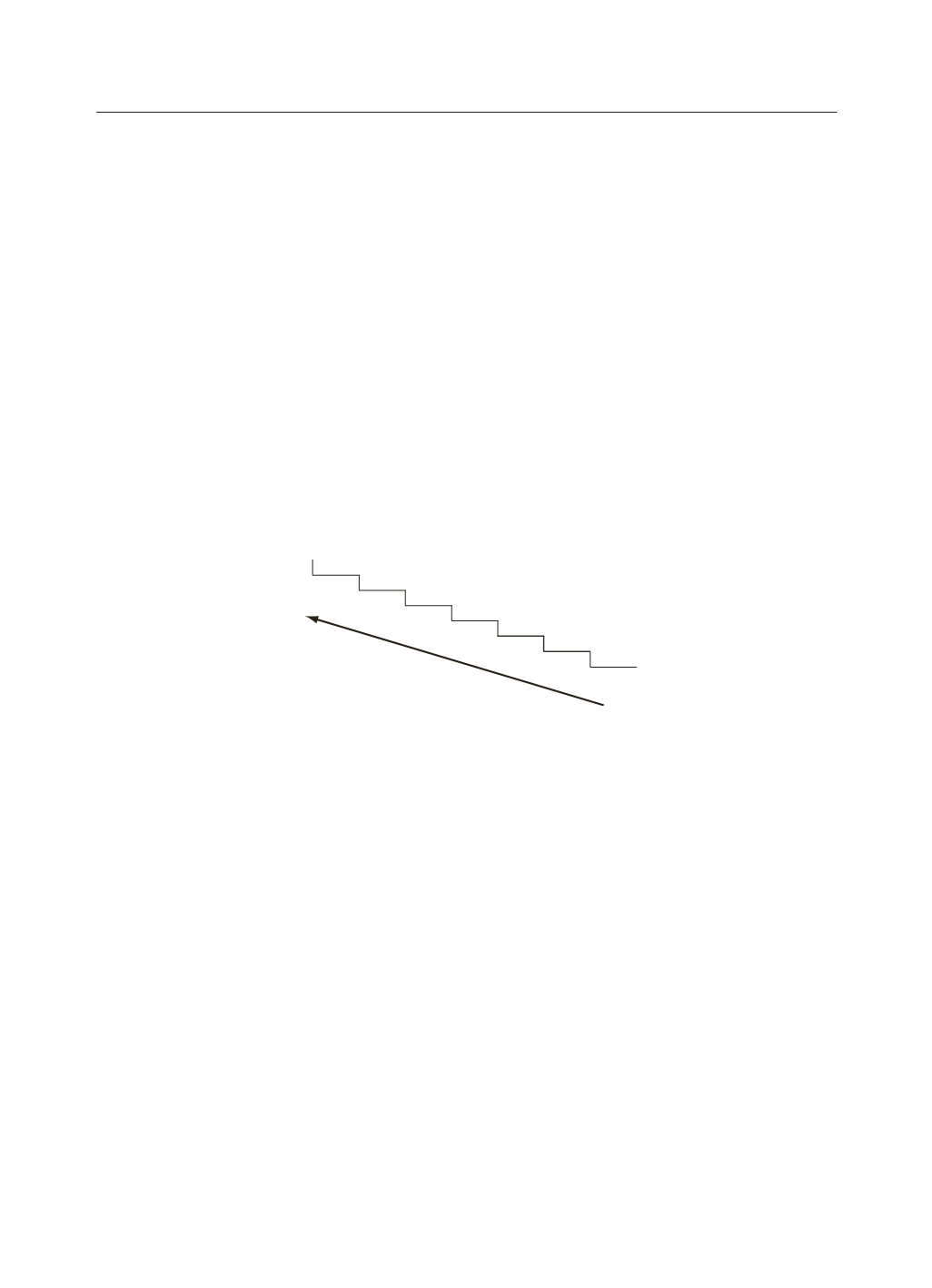
A questo punto si considerano i resti in ordine inverso rispetto a
come sono stati ottenuti durante le divisioni (dall’ultimo resto fino al
primo). A tale proposito si noti la freccia il cui verso va dal basso verso
l’alto e da destra verso sinistra. Si ottiene quindi la seguente sequenza di
resti: 1001000. Questa sequenza di cifre pari a 1 e 0 rappresenta il
numero 72 nel sistema binario.
Quindi (72)
10
= (1001000)
2
.
72
0
2
36
0
2
18
0
2
9
1
2
4
0
2
2
0
2
1
1
2
0
46
I sistemi di numerazione
















