
L’insieme
B
–
A
=
B
– (
A
∩
B
), in quanto togliere dall’insieme
B
tut-
ti gli elementi di
A
è equivalente a togliere i soli elementi che
B
ha in
comune con
A
. Quindi:
B
–
A
= {2, 6}
Se dall’insieme
A
∪
B
si tolgono gli elementi di
A
∩
B
e di
B
–
A
, si
ottengono i soli elementi dell’insieme
A
–
B
. Quindi:
A
–
B
= {4, 7}
Infine,
A
= (
A
–
B
)
∪
(
A
∩
B
), ossia gli elementi di
A
sono quelli che
appartengono solo ad
A
oppure ad
A
e
B
contemporaneamente. Quin-
di:
A
= {1, 3, 4, 5, 7}
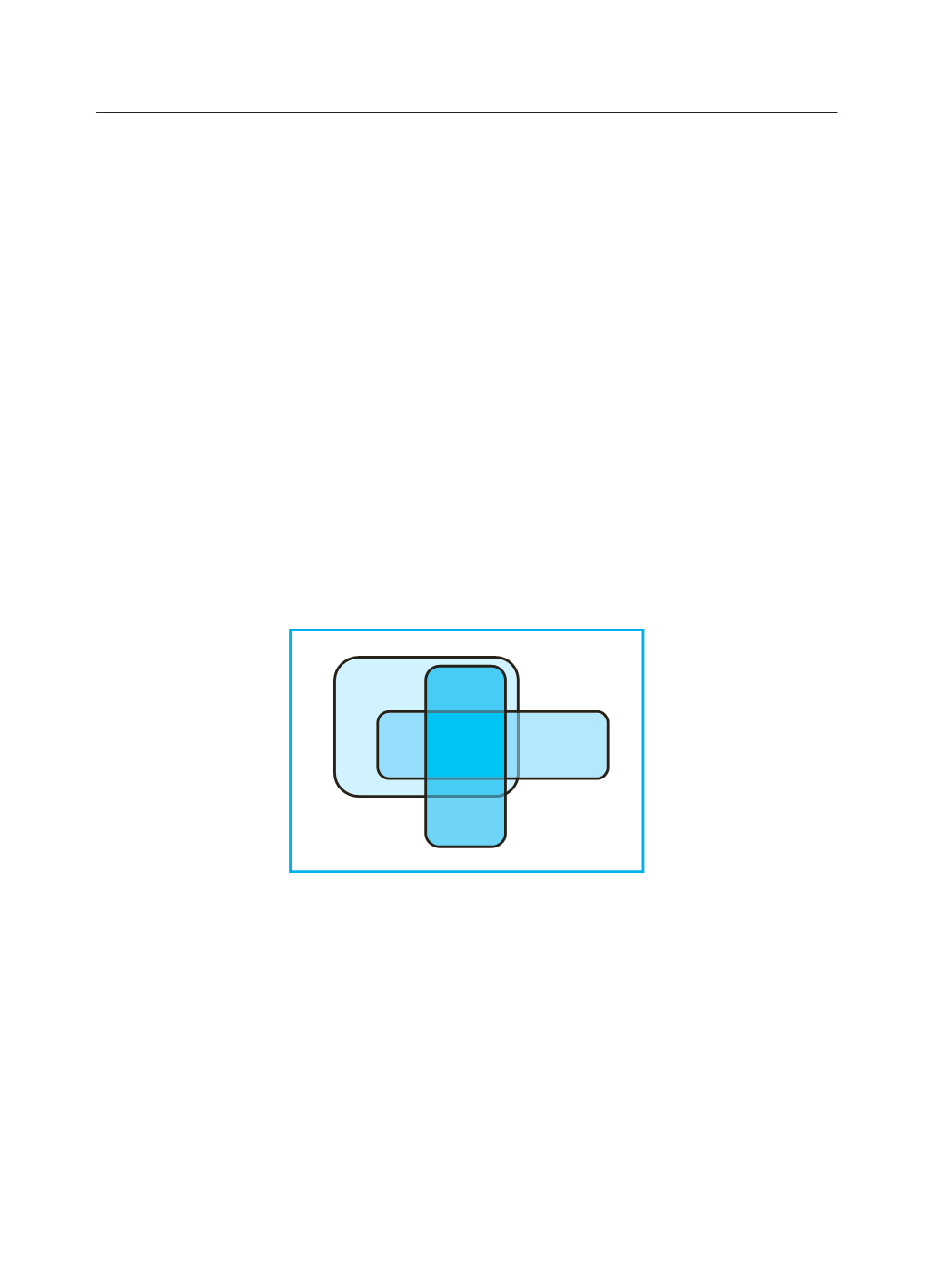
3) Dato il diagramma di Venn in figura, determinare i seguenti
insiemi:
A
∩
B
∩
C
,
A
∩
C
,
(
A
∩
C
) – (
B
∩
C
),
B
–
C
.
Osservato il diagramma, si ottiene:
A
∩
B
∩
C
= {
f
,
g
}
A
∩
C
= {
c
,
d
,
f
,
g
}
Inoltre, siccome
B
∩
C
= {
f
,
g
}, allora (
A
∩
C
) – (
B
∩
C
) = {
c
,
d
}.
B
–
C
= {
e
,
h
,
i
}
a
b
c d
e f g h i
l
m
A
B
C
4
Gli insiemi
















