
1. Gli insiemi
I punti-chiave
➢
Rappresentazione grafica degli insiemi.
➢
Le principali operazioni tra gli insiemi.
➢
Caratteristiche delle relazioni e delle funzioni.
1.1. Definizione
Il concetto di insieme costituisce l’elemento fondante di quella parte
della matematica che è la teoria degli insiemi. Con questo termine si
indica ogni raggruppamento, collezione, aggregato di elementi, indi-
pendentemente dalla loro natura.
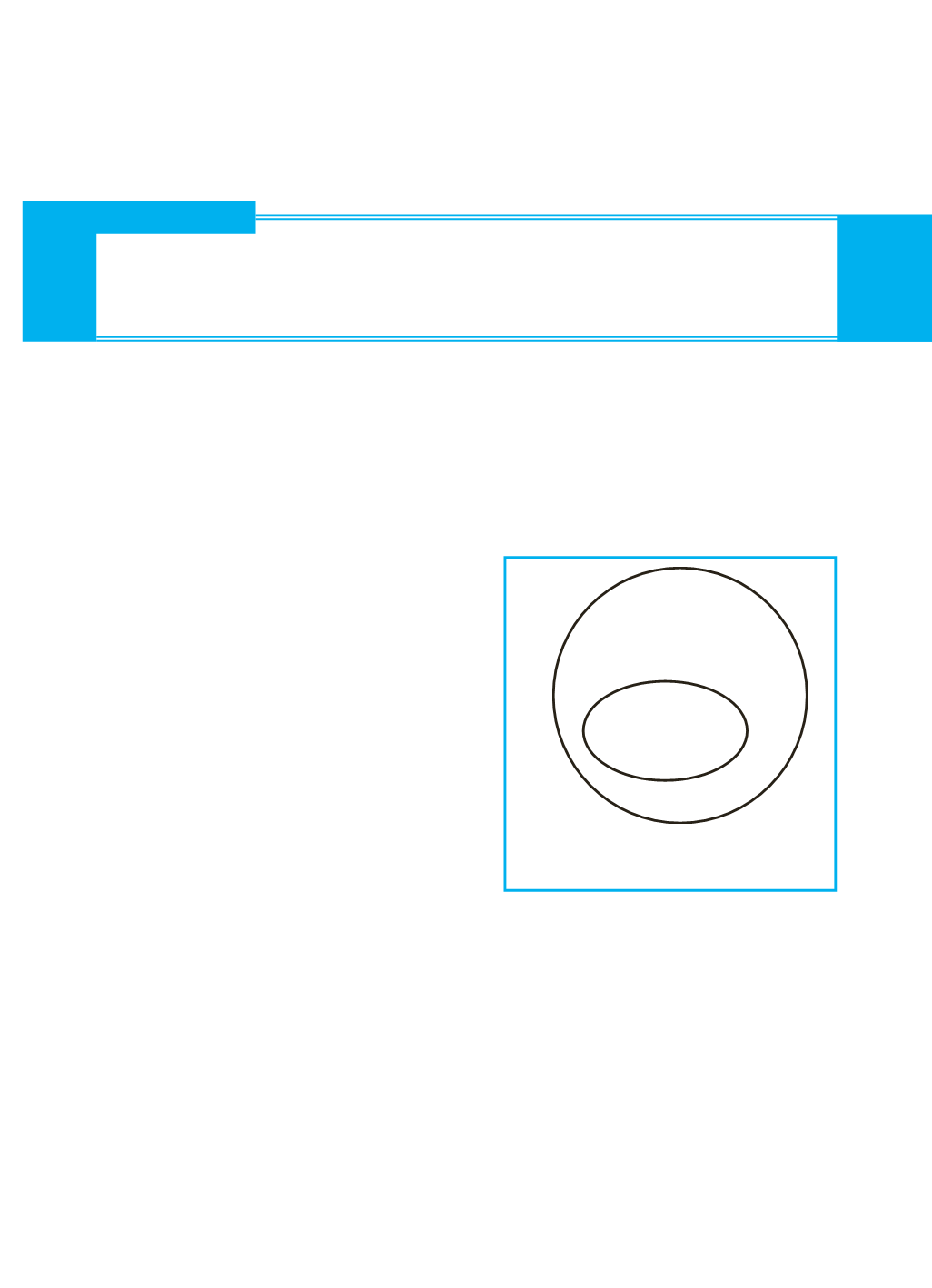
Un
diagramma di Eulero-Venn
(o semplicemente diagramma di
Venn) è una rappresentazione grafi-
ca di un insieme che consiste nel rac-
chiuderne gli elementi all’interno di
una linea chiusa non intrecciata
(Figura 1-1).
In Figura 1-1 l’insieme
A
è com-
posto dagli elementi indicati con
a
,
b
,
c
,
d
; questo viene indicato con la
notazione
A
= {
a
,
b
,
c
,
d
}. In riferi-
mento ad un singolo elemento del-
l’insieme, la notazione
a
∈
A
indica che l’elemento
a
“appartiene”
all’insieme
A
. Inoltre, gli elementi
b
e
c
appartengono all’insieme
A
che
è contenuto in
A
(la notazione usata è la seguente
A
⊂
A
). Per tale
motivo
A
è detto “sottoinsieme di
A
”.
1.2. Operazioni tra insiemi
Si considerano i due insiemi, mostrati in Figura 1-2,
A
= {
a
,
b
,
c
,
d
} e
B
= {
b
,
c
,
e
}.
L’
unione
tra i due insiemi è costituita da tutti gli elementi che si pos-
a
b
c
d
A’
A
Figura 1-1
L’insieme A e il sottoinsieme A
















