
192
Capitolo
7
Energia di un sistema
Pensiamo a un sistema costituito da un libro e dalla Terra, interagenti attraverso la
forza gravitazionale. Compiamo un certo lavoro sul sistema sollevando lentamente il
libro che compie uno spostamento verticale
D
r
S
= (
y
f
–
y
i
)
j
^
come mostrato nella Figu-
ra 7.15. In accordo con la nostra discussione sul lavoro inteso come trasferimento di
energia, il lavoro compiuto sul sistema deve manifestarsi come un aumento di energia
del sistema. Il libro è in quiete prima che compiamo il lavoro ed è in quiete dopo che
lo abbiamo compiuto. Quindi, non c’è variazione dell’energia cinetica del sistema.
Poiché la variazione di energia del sistema non compare nella forma di ener-
gia cinetica, deve essere immagazzinata come qualche altra forma di energia. Dopo
aver sollevato il libro, potremmo lasciarlo andare e farlo cadere #no alla posizione
iniziale
y
i
. Si noti che ora il libro (e quindi il sistema) possiede energia cinetica e la
causa di tale energia deriva dal fatto che si è compiuto lavoro nel sollevare il libro.
Possiamo dire che quando il libro si trova nella posizione più alta, l’energia del siste-
ma ha la
potenzialità
di diventare energia cinetica, che non si manifesta #nché non
lasciamo cadere il libro. Pertanto, il meccanismo di immagazzinamento di energia
prima che il libro venga lasciato cadere è chiamato
energia potenziale
. Scopriremo
che l’energia potenziale di un sistema può essere associata solo a particolari tipi di
forze agenti tra i costituenti. La quantità di energia potenziale del sistema è deter-
minata dalla
con!gurazione
del sistema. Spostando i membri del sistema in posizioni
differenti o ruotandoli, possiamo variare la con#gurazione del sistema e quindi la
sua energia potenziale.
Deriviamo ora una espressione per l’energia potenziale associata ad un oggetto
che si trova in una data posizione al di sopra della super#cie terrestre. Consideria-
mo un agente esterno che solleva un corpo di massa
m
da un’altezza iniziale
y
i
ad
un’altezza #nale
y
f
come nella Figura 7.15. Assumiamo che il sollevamento avvenga
lentamente, senza accelerazione, di modo che la forza applicata dall’agente esterno
sia uguale in modulo alla forza gravitazionale agente sul corpo: il corpo è schematiz-
zato come un punto materiale in equilibrio in moto con velocità costante. Il lavoro
compiuto dall’agente esterno sul sistema (corpo e Terra) quando il corpo viene
spostato verso l’alto è dato dal prodotto della forza applicata verso l’alto
F
S
app
per lo
spostamento verso l’alto di tale forza,
D
r
S
=
D
y
j
^
:
W
est
5
1
F
S
app
2
?
D
r
S
5
1
mg
j
^
2
?
3 1
y
f
2
y
i
2
j
^
4
5
mgy
f
2
mgy
i
(7.18)
Tale risultato rappresenta il lavoro complessivo compiuto sul sistema dato che la forza
applicata è la sola forza sul sistema da parte dell’ambiente. (Ricordate che la forza
gravitazionale è una forza
interna
al sistema.) Si noti la somiglianza tra l’Equazione
7.18 e l’Equazione 7.15. In ciascuna delle equazioni il lavoro compiuto sul sistema è
uguale alla differenza tra i valori #nale e iniziale di una certa grandezza. Nell’Equa-
zione 7.15 il lavoro rappresenta un trasferimento di energia nel sistema e l’incremen-
to dell’energia del sistema si manifesta sotto forma di energia cinetica. Nell’Equazio-
ne 7.18 il lavoro rappresenta un trasferimento di energia nel sistema e l’energia del
sistema si manifesta in una forma diversa, che abbiamo chiamato energia potenziale.
Pertanto possiamo identi#care la quantità
mgy
come l’
energia potenziale gravita-
zionale
U
g
di un sistema di un corpo di massa
m
e della Terra:
U
g
;
mgy
(7.19)
L’energia potenziale gravitazionale si misura in joule, cioè nelle stesse unità del lavo-
ro e dell’energia cinetica. L’energia potenziale, come il lavoro e l’energia cinetica, è
una quantità scalare. Si noti che l’Equazione 7.19 è valida solo per corpi in prossimi-
tà della super#cie terrestre, dove
g
è approssimativamente costante.
3
Usando la nostra de#nizione di energia potenziale gravitazionale, l’Equazione
7.18 può essere riscritta nella forma:
W
est
5 D
U
g
(7.20)
che matematicamente dice che il lavoro esterno compiuto sul sistema in questa situa-
zione si manifesta come variazione dell’energia potenziale gravitazionale del sistema.
L’Equazione 7.20 è simile nella forma all’Equazione 7.17 teorema dell’energia
cinetica (o teorema delle forza vive). Nell’Equazione 7.17, il lavoro è compiuto sul si-
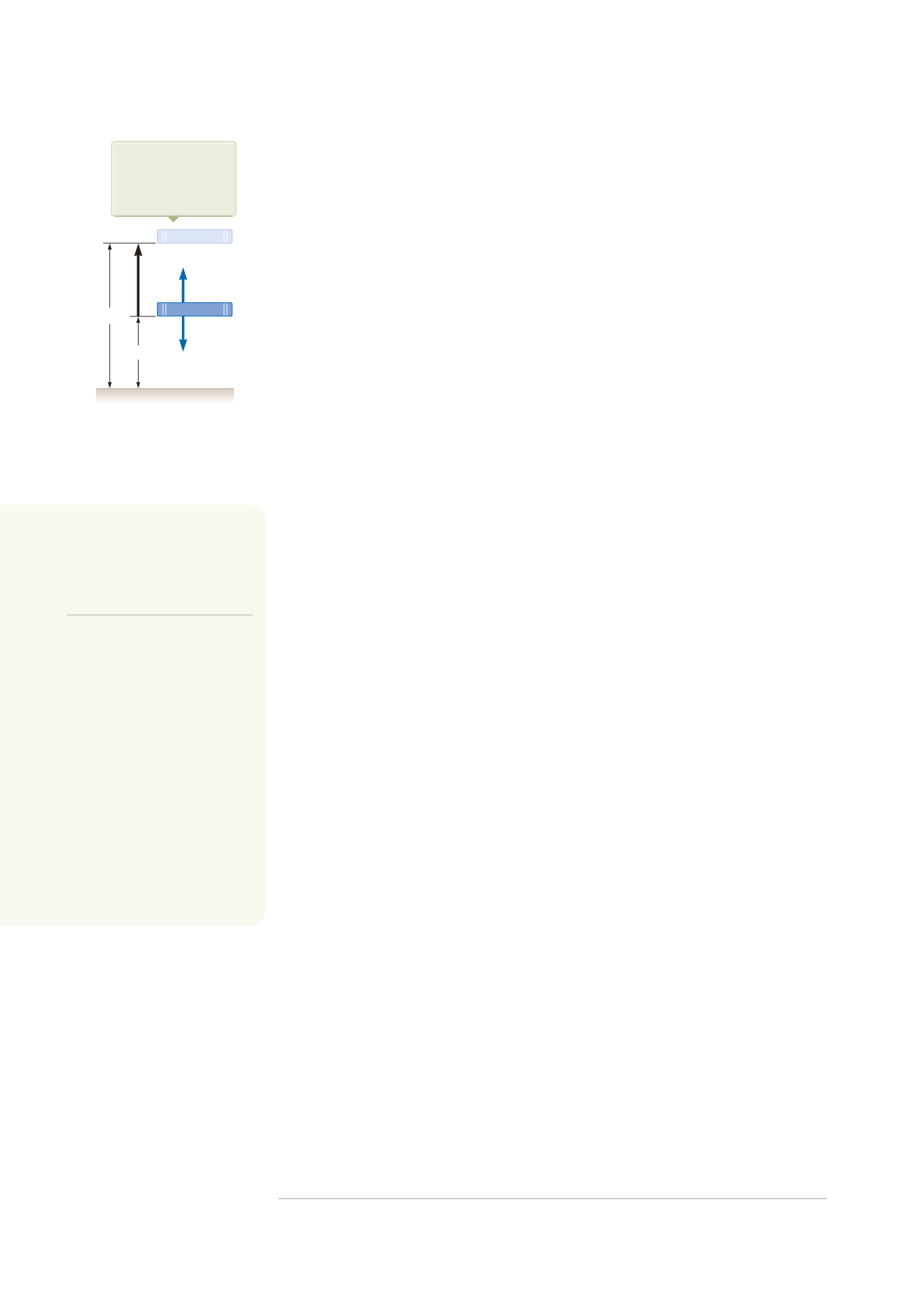
Figura 7.15
Un agente esterno
solleva il libro lentamente da
un’altezza
y
i
ad un’altezza
y
f
.
y
f
y
i
m
D
Fisica
Fisica
Il lavoro compiuto da
una forza agente sul
sistema libro-Terra è
mgy
f
2
mgy
i
.
F
app
S
r
S
g
S
Prevenire l’errore 7.7
Energia potenziale
L’espressione
energia potenziale
non si riferisce
a qualcosa che potenzialmente
può diventare energia. L’energia
potenziale è energia.
Prevenire l’errore 7.8
L’energia potenziale si riferisce ad
un sistema.
L’energia potenziale
è sempre associata ad un
sistema
di due o più corpi interagenti tra
loro. Quando un piccolo corpo si
muove in prossimità della superfi-
cie terrestre sotto l’influenza della
gravità, possiamo a volte parlare
di energia potenziale “associata
al corpo” piuttosto che “associata
al sistema”, come sarebbe più cor-
retto; questo è giustificato dal
fatto che la Terra non subisce uno
spostamento apprezzabile. Tutta-
via noi non parleremo di energia
potenziale “del corpo” poiché que-
sto modo di dire non tiene conto
del ruolo della Terra.
3
L’assunzione che
g
sia costante è valida finché gli spostamenti verticali del corpo sono piccoli rispetto al raggio
della Terra.
Energia potenziale
X
gravitazionale
















