
b)
D
m
< 0, massa finale minore di quella iniziale
⇒
D
E
k
> 0, nello stato finale c’è
più energia cinetica, una parte dell’energia di massa iniziale si è trasformata in
energia cinetica.
Questa nozione della non immutabilità della massa e della possibilità di
conversio-
ne tra massa ed energia
è una delle più importanti introdotte dalla teoria della rela-
tività.
Dalle trasformazioni di massa in energia nelle reazioni di fusione tra nuclei
degli isotopi dell’idrogeno si spera di ottenere una fonte di energia praticamente
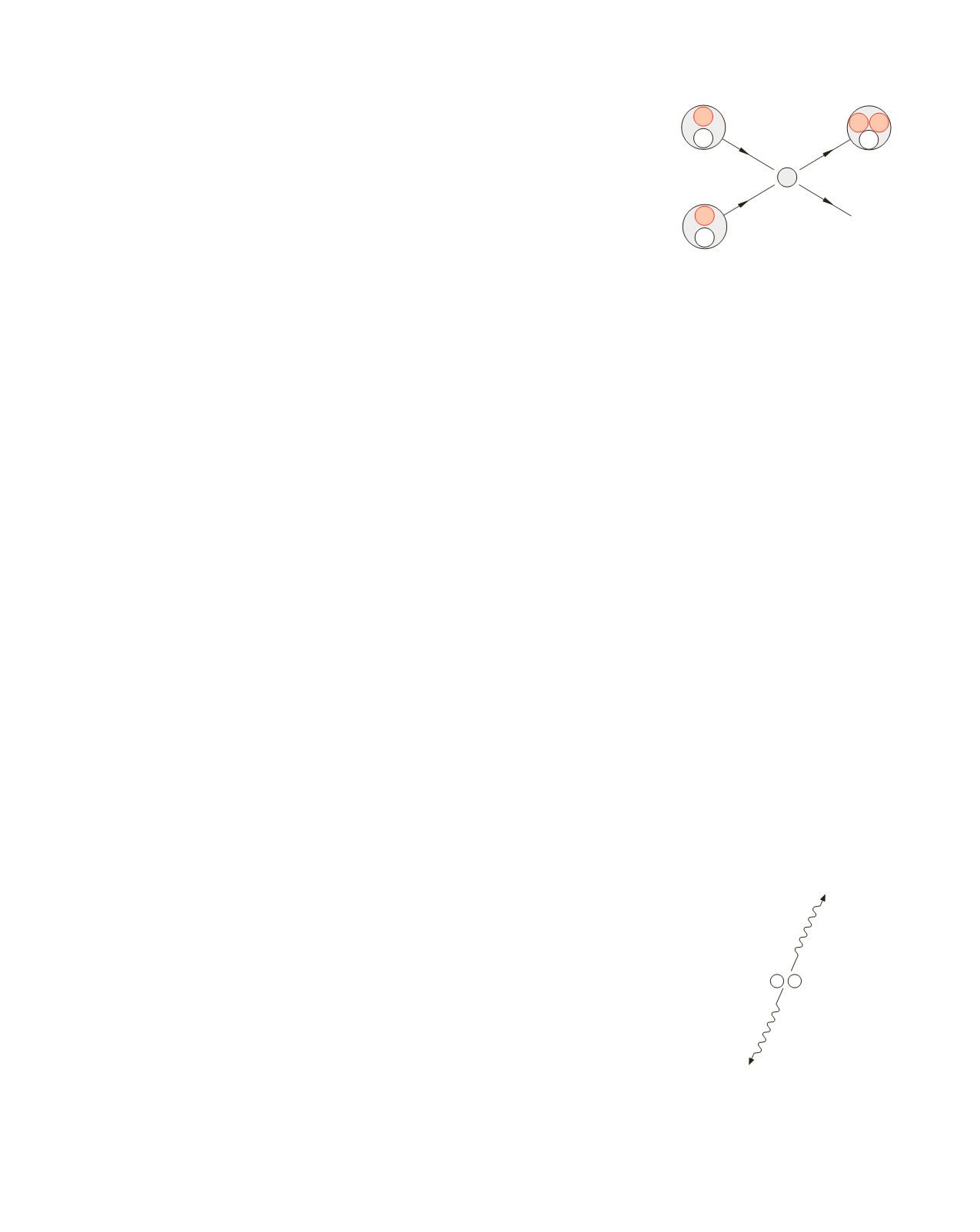
inesauribile. L’esempio più semplice è costituito dalla fusione di due nuclei di deu-
terio, detti deutoni, ciascuno formato da un protone e da un neutrone, che danno
luogo a un
nucleo di elio
3 e ad un neutrone; l’elio 3 è un isotopo dell’elio con
nucleo composto da due protoni e da un neutrone. La somma delle masse della par-
ticelle finali è minore di quella dei due nuclei di deuterio e la differenza si ritrova
sotto forma di energia cinetica dell’elio 3 e del neutrone; è proprio l’energia cineti-
ca del neutrone che verrebbe successivamente assorbita e trasformata in altre forme
di energia utilizzabile. Si osservi che la reazione non avviene spontaneamente per-
ché i due deutoni sono entrambi carichi positivamente e si respingono; essi devono
perciò possedere una certa energia che permetta di vincere la repulsione elettrica.
La via sperimentale attualmente più seguita è di portare deuterio gassoso a tempe-
rature molto elevate, il che corrisponde a energie cinetiche elevate come vedremo
nel capitolo sulle proprietà dei gas, con lo scopo di favorire il processo di fusione.
Si parla di
fusione termonucleare controllata
e al momento attuale alcuni dei reat-
tori sperimentali operanti nel mondo non sono lontani dalla parità nel bilancio ener-
getico, cioè dall’eguaglianza tra energia spesa complessivamente per realizzare le
fusioni e energia ricavata dalle fusioni. Però la via da percorrere per realizzare
un’operazione continua e affidabile sembra ancora molto lunga.
Sempre a reazioni di fusione si attribuisce la fonte di energia di alcune categorie
di stelle, tra cui il Sole.
Un altro esempio interessante è la formazione di uno stato legato a partire da
due particelle singole, per esempio un protone e un neutrone che danno un deutone
(nucleo del deuterio). La massa del deutone è inferiore alla somma delle masse del
protone e del neutrone, però il sistema è legato con una certa energia. Si misura che
l’energia di legame vale proprio (
D
m
)
c
2
: la massa scomparsa si è tramutata in ener-
gia. Rompendo il sistema si deve spendere energia e si recupera massa.
Infine vogliamo ricordare un processo che ha un’applicazione in campo medi-
co. Alcune sostanze radioattive emettono positroni, particelle aventi la stessa
massa dell’elettrone e carica opposta. Quando un positrone così prodotto attraversa
la materia avviene un processo di annichilazione: il positrone interagisce con un
elettrone, entrambi scompaiono e vengono emessi due fotoni, aventi energia pari
all’energia di massa delle particelle scomparse. In prima approssimazione possia-
mo supporre che l’energia cinetica iniziale sia trascurabile rispetto all’energia di
massa e fare questa schematizzazione:
– in un punto si ha l’annichilazione, con le particelle praticamente in quiete, e
viene resa disponibile l’energia 2
mc
2
;
– da quel punto escono due fotoni, aventi la stessa direzione di moto e verso
opposto, ciascuno di energia
mc
2
.
Si ha trasformazione integrale di massa in energia (ricordiamo che i fotoni hanno
massa nulla).
È noto in medicina che, iniettando nel corpo umano alcuni particolari composti
chimici, questi si accumulano in organi o tessuti specifici, come il muscolo cardia-
co o tessuti con cellule tumorali. Sostituendo in una piccola percentuale di moleco-
le di tali composti certi atomi con loro isotopi radioattivi emettitori di positroni (ad
esempio
C
11
al posto di
C
12
), con il che non si alterano le proprietà di assorbimento
da parte dell’organismo, si ottiene una concentrazione di emissione nelle zone inte-
Quantità di moto ed energia relativistiche
127
p
p
p p
n
n
n
n
d
+
d
→
n
+
3
He
Figura 3.24
Fotone
Fotone
Positrone + – Elettrone
Figura 3.25
















