
!!
CAPITOLO +!
|
Macchine termiche, entropia e secondo principio della termodinamica
e vediamo che il lavoro
W
mac
compiuto dalla macchina termica è uguale al-
l’energia totale assorbita dalla macchina. Come possiamo vedere dalla Figura 18.1,
Q
tot
5
|
Q
c
| 2
|
Q
f
|
. Quindi,
W
mac
5
|
Q
c
| 2
|
Q
f
|
12.1
b
Se la sostanza impiegata è un gas, il lavoro totale svolto in una trasformazione cicli-
ca è l’area racchiusa dalla curva che rappresenta la trasformazione in un diagramma
PV
. Quest’area è mostrata per una trasformazione ciclica arbitraria nella Figura 18.2.
Il
rendimento
,
e
, di una macchina termica è de#nito come il rapporto fra il lavoro
svolto dalla macchina e l’energia assorbita alla temperatura più alta durante un ciclo:
e
5
W
mac
u
Q
c
u
5
u
Q
c
u
2
u
Q
f
u
u
Q
c
u
5
1
2
u
Q
f
u
u
Q
c
u
12.4
b
Possiamo considerare il rendimento come il rapporto fra ciò che si ottiene (trasfe-
rimento di energia sotto forma di lavoro) e ciò che si spende (trasferimento di energia
dal termostato di alta temperatura). L’Equazione 18.2 mostra che una macchina ter-
mica avrebbe un rendimento del 100% (
e
5
1) soltanto se
Q
f
5
0 (cioè se non venisse
trasferita energia al termostato freddo). In altre parole, una macchina termica con ren-
dimento unitario dovrebbe trasformare tutta l’energia assorbita in lavoro meccanico.
L’
enunciato di Kelvin-Planck del
secondo
principio
della
termodinamica
può
esprimersi come segue:
È impossibile costruire una macchina termica che, operando in un ciclo, abbia
come unico risultato quello di assorbire energia da un termostato e di produrre
una uguale quantità di lavoro.
L’essenza di questo enunciato del secondo principio è che è teoricamente impossi-
bile costruire una macchina come quella della Figura 18.3 che lavora col 100% di ren-
dimento. Tutte le macchine devono scaricare una parte di energia
Q
f
nell’ambiente.
QUIZ RAPIDO
!.
L’energia in ingresso ad una macchina è 3.00 volte maggiore del
lavoro che produce. (
i
) Qual è il suo rendimento? (a) 3.00 (b) 1.00 (c) 0.333
(d) impossibile da calcolare (
ii
) Che frazione dell’energia in ingresso viene ceduta al
termostato freddo? (a) 0.333 (b) 0.667 (c) 1.00 (d) impossibile da determinare.
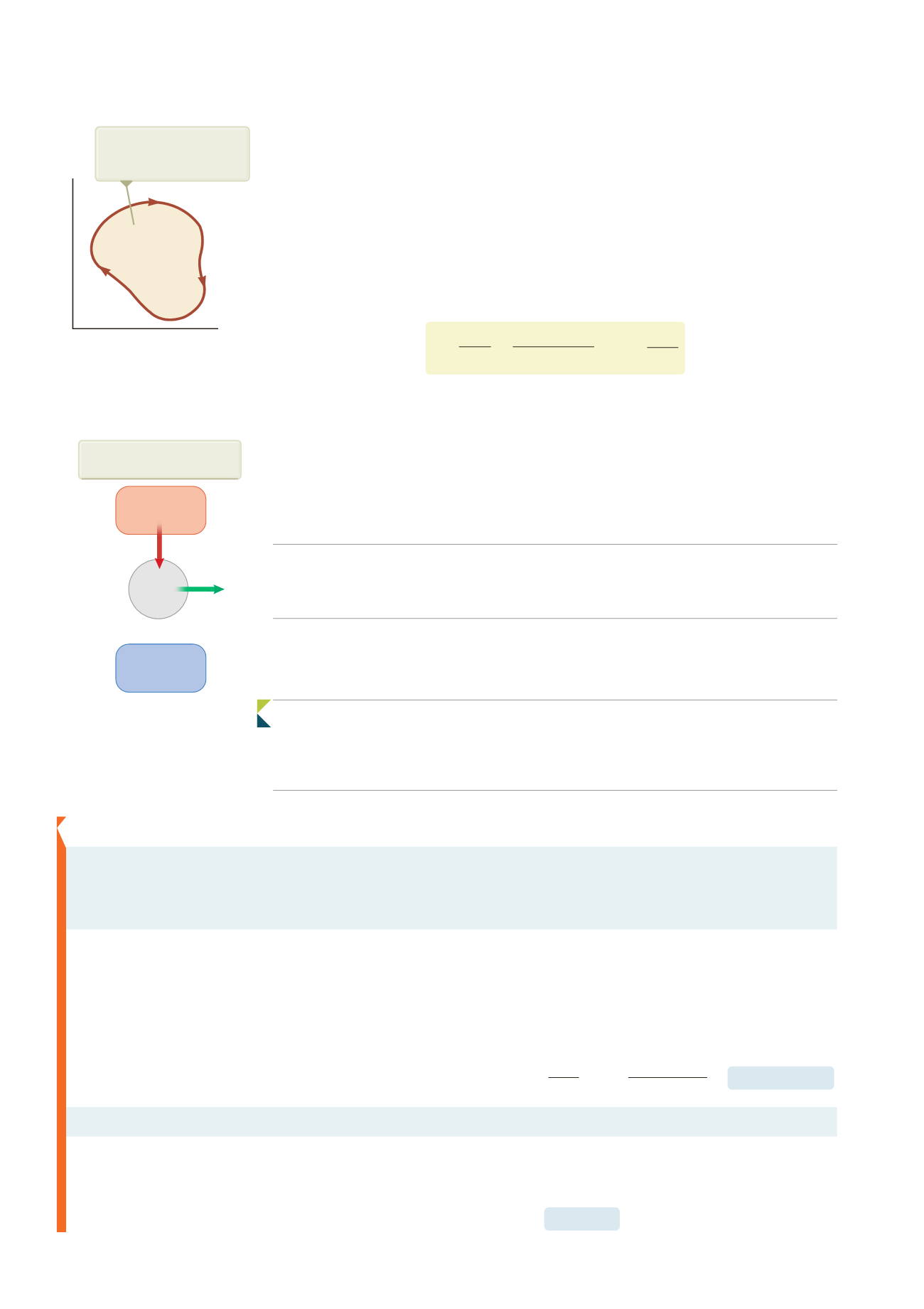
P
V
Area =
W
mac
L’area racchiusa è pari al
lavoro complessivo
compiuto.
Figura +!.9
Diagramma
PV
per
un processo ciclico arbitrario.
Q
c
Termostato
caldo
a
T
c
Termostato
freddo
a
T
f
Macchina
termica
W
mac
Una macchina termica
impossibile
Figura +!.:
Diagramma
schematico di una macchina
termica che prende energia da
un termostato caldo e la converte
tutta in lavoro. È impossibile
costruire tale motore perfetto.
Esempio
!.
|
Rendimento di un motore
Un motore compie una trasformazione assorbendo 2.00
3
10
3
J di energia da un termostato caldo durante un ciclo
e cedendo 1.50
3
10
3
J a un termostato freddo.
(A)
Trovare il rendimento del motore.
SOLUZIONE
Concettualizzazione
Riguardate la Figura 18.1; pensate all’energia che entra nel motore dal termostato caldo e che
si divide in una parte che produce lavoro e un’altra parte che viene ceduta sotto forma di calore al termostato freddo.
ClassiHcazione
Questo esempio comporta la valutazione di quantità dalle equazioni introdotta in questo paragrafo,
sicché lo consideriamo come un problema da risolvere per sostituzione.
Ricaviamo il rendimento del motore usando l’Equazione 18.2:
e
5
1
2
u
Q
f
u
u
Q
c
u
5
1
2
1.50
3
10
3
J
2.00
3
10
3
J
5
0.250, o 25.0%
(B)
Quanto lavoro compie questo motore in un ciclo?
SOLUZIONE
Il lavoro svolto è la differenza fra l’energia in entrata e in uscita:
W
mac
5
)
Q
c
)
2
)
Q
f
)
5
2.00
3
10
3
J
2
1.50
3
10
3
J
5
5.0
3
10
2
J
















