
24.3
Applicazione della legge di Gauss a varie distribuzioni di carica
731
24.3
Applicazione della legge di Gauss a varie
distribuzioni di carica
Come osservato in precedenza, la legge di Gauss è utile per determinare i campi
elettrici quando la distribuzione di carica è caratterizzata da un alto grado di
simmetria. Gli esempi che seguonomostrano come scegliere una superficie gaussiana
sulla quale l’integrale di superficie dato dall’Equazione 24.6 risulta semplificato e il
campo elettrico può essere determinato. Nella scelta della superficie si deve sempre
utilizzare la simmetria della distribuzione di cariche, in modo che
E
possa essere
portato fuori dall’integrale. In questo tipo di calcoli è fondamentale la scelta di una
superficie chiusa opportuna costituita da porzioni di superficie che soddisfano una
o più delle seguenti condizioni:
1.
Da considerazioni di simmetria si può arguire che il valore del campo
elettrico deve essere costante sulla porzione di superficie.
2.
Il prodotto scalare nell’Equazione 24.6 può essere espresso come un
semplice prodotto algebrico
E dA,
in quanto
E
S
e
d
A
S
sono paralleli.
3.
Il prodotto scalare nell’Equazione 24.6 è nullo, in quanto
E
S
e
d
A
S
sono
perpendicolari.
4.
Il campo elettrico è nullo sulla porzione di superficie.
Differenti parti che costituiscono la superficie gaussiana possono soddisfare
differenti condizioni, purché per ciascuna porzione sia verificata almeno una delle
proprietà indicate. Tutte queste quattro condizioni vengono utilizzate negli esempi
discussi nella parte rimanente del capitolo. Se la distribuzione di cariche non ha una
simmetria che permette di soddisfare queste condizioni, la legge di Gauss continua
a rimanere valida, ma non può essere usata per determinare il campo elettrico
generato dalla distribuzione di carica.
S O L U Z I O N E
Prevenire l’errore 24.2
Le superfici gaussiane non sono reali
Una superficie gaussiana è una super-
ficie immaginaria, costruita in modo
da soddisfare le condizioni qui elen-
cate. Non coincide necessariamente
con una superficie reale.
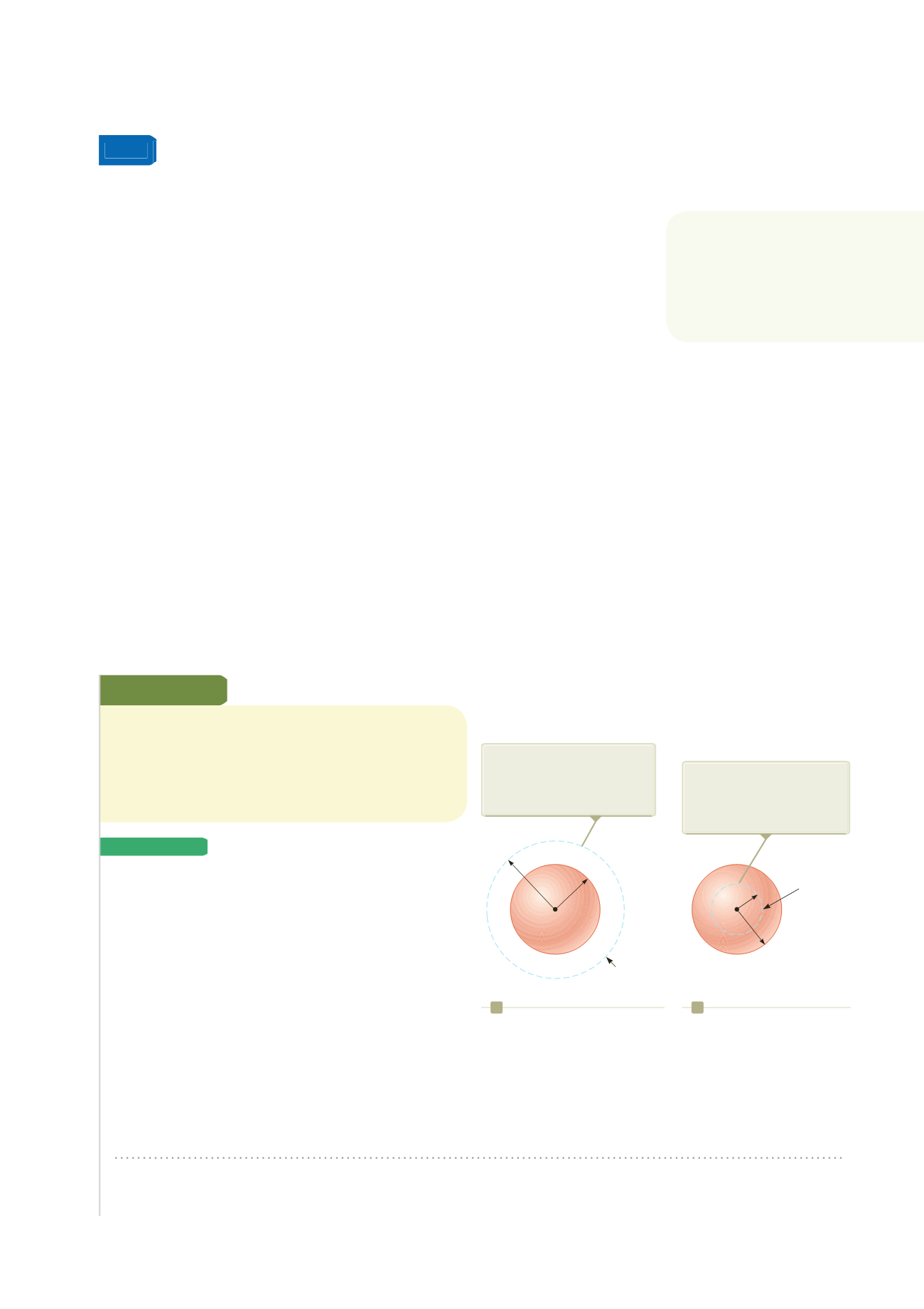
Sfera
gaussiana
Sfera
gaussiana
Per i punti all’esterno della
sfera è disegnata una superficie
gaussiana concentrica alla
sfera.
Per i punti all’interno della
sfera è disegnata una super-
ficie gaussiana sferica più
piccola della sfera.
r
a
r
a
Q
a
b
Figura 24.10
(Esempio 24.3) Una sfera isolante uniformemente
carica di raggio
a
e carica totale
Q
. Nelle figure come questa la
linea tratteggiata rappresenta l’intersezione tra la superficie gaus-
siana ed il piano della pagina.
Esempio
24.3
Distribuzione di carica a simmetria sferica
Una sfera isolante di raggio
a
possiede una densità
volumetrica di carica uniforme
r
e la carica positiva
totale è
Q
(Fig. 24.10).
(A)
Si calcoli l’intensità del campo elettrico in un
punto all’esterno della sfera.
Concettualizzare
Si noti che questo problema diffe-
risce dalle nostre precedenti discussioni sulla legge di
Gauss. Lo studio del campo elettrico generato da cari-
che puntiformi è stato affrontato nel Paragrafo 24.2.
Qui siamo interessati al campo elettrico generato da
una distribuzione di carica. Abbiamo già trovato il
campo prodotto da diverse distribuzioni di carica nel
Capitolo 23 integrando su tutta la distribuzione. Que-
sto esempio illustra una differenza rispetto alla nostra
discussione nel Capitolo 23. In questo capitolo ricave-
remo il campo elettrico utilizzando la legge di Gauss.
Classificare
Dal momento che la carica
Q
è distribuita
uniformemente all’interno della sfera, la distribuzione
di carica presenta simmetria sferica ed è possibile applicare
la legge di Gauss per trovare il campo elettrico.
Analizzare
In accordo con la simmetria sferica della distribuzione di carica, si sceglie una superficie gaussiana ancora
sferica di raggio
r
e concentrica alla sfera, come in Figura 24.10a. Con questa scelta è soddisfatta dovunque sulla super-
ficie la condizione (2) e
E
S
·
d
A
S
= E dA.
segue
















