
v(
t
) =
g
·
t
(dalla 2.13 con v
0
= 0) (2.15)
(dalla 2.14 con x
0
= 0, v
0
= 0) (2.16)
dove
x
(
t
), che è la posizione del corpo nel generico istante
t
, indica lo spazio
percorso a partire dalla posizione iniziale x
0
= 0.
Segue che
dove
t
è il tempo di caduta
(2)
:
(2.17)
La velocità raggiunta dal corpo nell’istante in cui tocca terra si ricava sosti-
tuendo l’espressione del tempo di caduta
t
nella (2.15):
(2.18)
Si consideri ora un corpo lanciato verso l’alto con velocità iniziale v
0
(Fig.
2.7). Considerando un sistema di coordinate tale che il verso positivo dell’asse
x
sia quello verso l’alto e l’origine (
x
0
= 0) si trovi nella posizione iniziale, il
moto del corpo è uniformemente decelerato e le relazioni che regolano tale
moto possono essere riscritte come:
v(
t
) = v
0
–
g
·
t
(il segno meno tiene conto del fatto che la velocità
(verso l’alto)
e l’accelerazione di gravità (verso il basso)
hanno verso opposto) (2.19)
(per
x
0
= 0 e versi opposti di velocità e accelerazio-
ne di gravità) (2.20)
2
2
1 )(
tg tx
◊
=
2
2
1
tg h
◊
=
g
h t
2
=
gh
2 v
=
2
0
2
1 v )(
tg t
tx
◊
-◊
=
Capitolo 2
Cinematica
725
www.
edises
.it
g
x
0
= 0
v
h
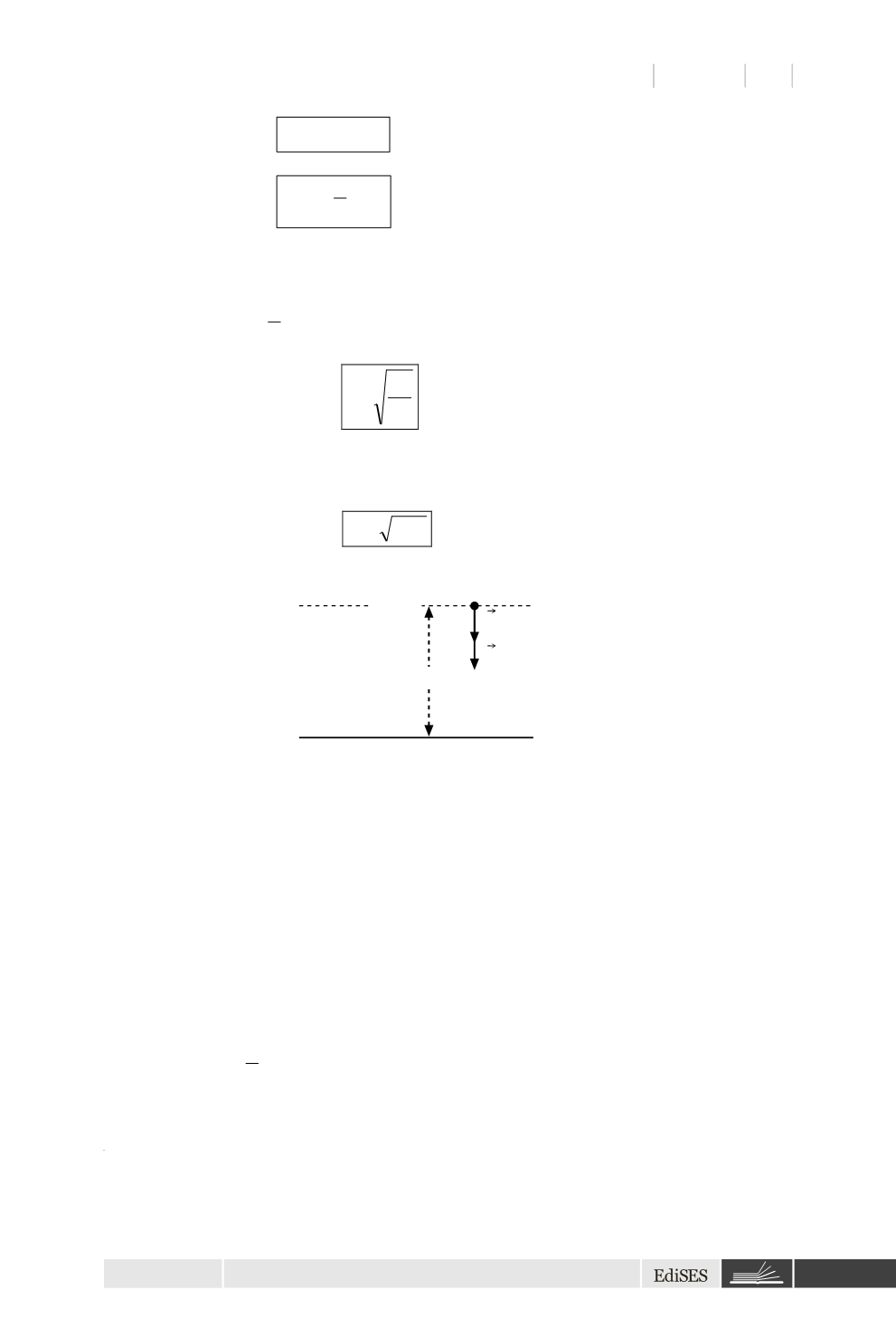
Figura 2.6
Caduta di un grave per effetto della attrazione gravitazionale.
(2)
Si può notare che in assenza di attrito il tempo di caduta è indipendente dalla natura del
corpo che cade. Il tempo di caduta dipende dalla quota di partenza.
















