
8
PROVE UFFICIALI
www.
edises
.it
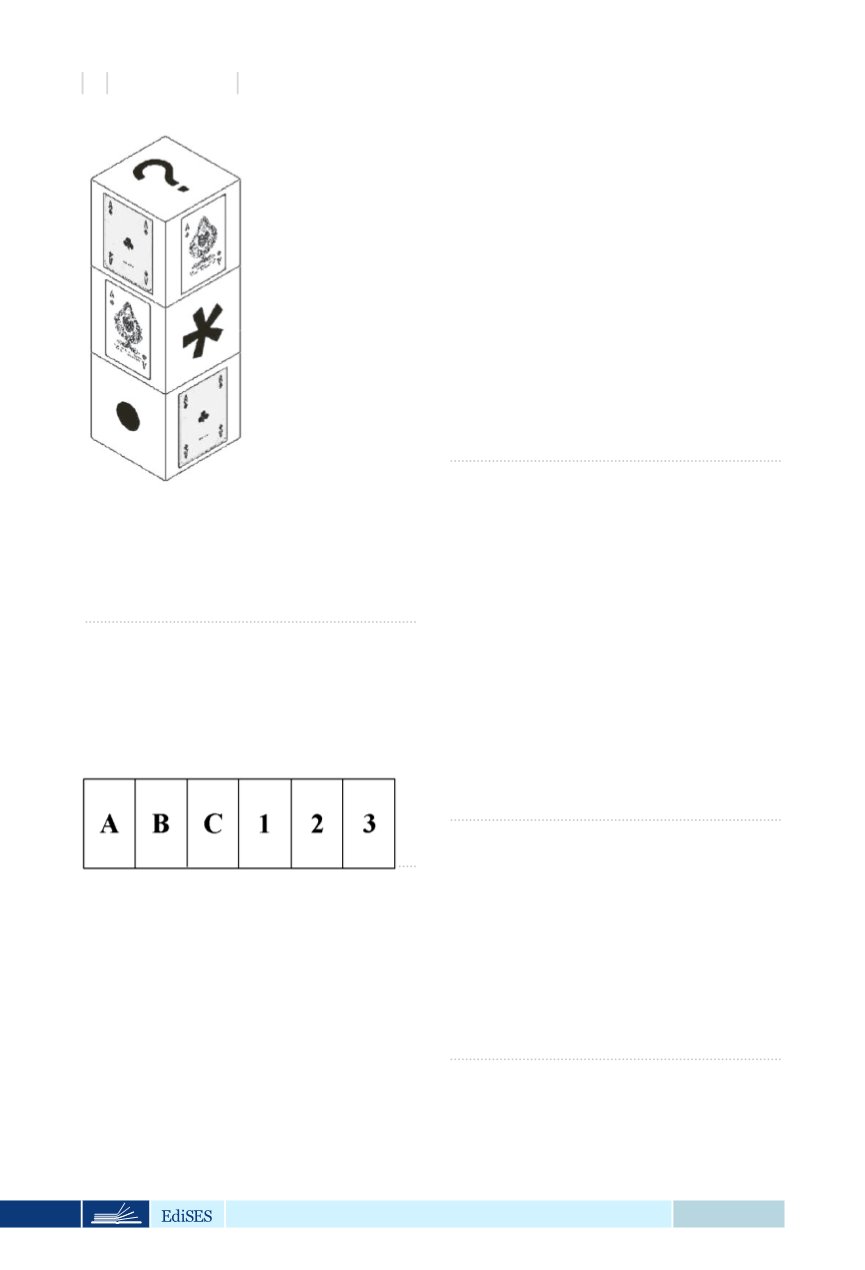
A. Pallino
B. Asso di cuori oppure asso di quadri
C. Asterisco oppure pallino
D. Asterisco
E. Asso di cuori
29) Prese da un mazzo particolare 6
carte, ciascuna delle quali su un lato
porta scritto una fra le lettere A, B, C e
sull’altro porta scritto una fra le cifre 1,
2, 3, Leo dispone sul tavolo le carte nel
modo seguente:
ed afferma:
Se una carta porta la lettera B su un lato,
sull’altro lato porta la cifra 2.
Qual è il numero minimo di carte che
Maria deve girare per essere sicura che
Leo afferma il vero?
A. 1
B. 6
C. 3
D. 2
E. 4
30) Del numero intero
n
sappiamo che
è compreso tra 2 e 6 (precisamente 2 ≤ n
≤ 6) e che rende vera una e una sola delle
seguenti affermazioni:
n
è divisibile per 4
n
è divisibile per 6
n
è divisibile per 2
n
è un divisore proprio di 6
Qual è il valore di
n
?
A. 6
B. 3
C. 5
D. 4
E. 2
31) Nell’harem del sultano Alì Babà i
4/5 delle odalische hanno i capelli neri
ed i 3/4 hanno gli occhi neri. Si può con-
cludere che:
A. almeno 11/20 delle odalische hanno
sia capelli che occhi neri
B. 3/5 delle odalische hanno sia capelli
che occhi neri
C. al più 11/20 delle odalische hanno sia
capelli che occhi neri
D. 4/5 delle odalische hanno sia capelli
che occhi neri
E. 3/4 delle odalische hanno sia capelli
che occhi neri
32) Ho a disposizione tanti cubi quanti
ne voglio e dipingo ogni loro faccia con i
colori rosso o verde. Quanti cubi diversi
posso ottenere?
A. 24
B. 6
C. 64
D. 36
E. 10
33) Gianni ha trovato un vecchio gior-
nale enigmistico che riportava uno sche-
ma triangolare in cui ogni numero, dal-
la seconda riga in giù, era uguale alla
somma dei due numeri situati sopra al
















