
www.
edises
.it
206
Parte Seconda
Area logico-matematica
A tale proposito, si consiglia di imparare l’ordine numerico dell’alfabeto, cioè A = 1,
B = 2 e così via come riportato di seguito:
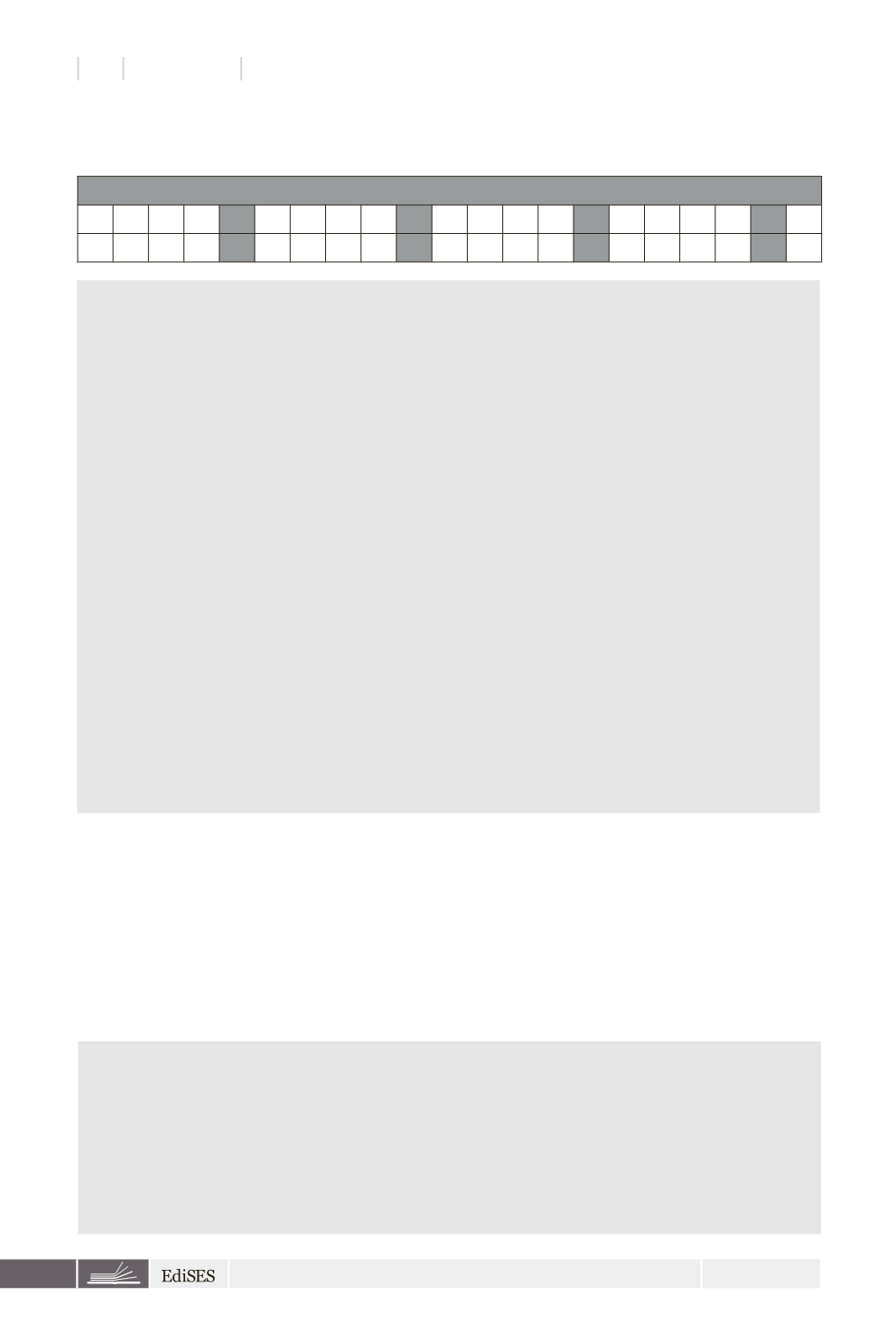
Alfabeto italiano (prima riga) e corrispondenti numeri d’ordine (seconda riga)
A B C D E F G H I L M N O P Q R S T U V Z
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21
Esempio
Completare la seguente successione utilizzando l’alfabeto italiano: M; H; ?; G; I; F
A. L
B. N
C. O
D. E
E. S
La risposta esatta è la
A
.
Convertiamo la serie alfabetica data nella corrispondente serie numerica:
M H ? G I F
11 8 ? 7 9 6
Nella serie, occorre considerare la distanza tra le lettere o, equivalentemente, tra i numeri cor-
rispondenti.
La relazione tra i numeri di posto pari è diversa da quella che lega i numeri di posto dispari. In
particolare:
1. I numeri di posto pari si ottengono sottraendo 3 dai numeri di posto dispari immediatamente
precedenti.
2. I numeri di posto dispari si ottengono aggiungendo 2 ai numeri di posto pari immediatamente
precedenti.
Seguendo tale criterio, la lettera incognita (la terza della serie) si ottiene avanzando di 2 posizioni
nell’alfabeto a partire dalla lettera H, ottenendo la lettera
L
.
4.2.2
Le serie alfanumeriche
Le
serie alfanumeriche
sono costituite da successioni di lettere e numeri in cui pos-
sono esistere nessi logici tra le lettere e tra i numeri in maniera disgiunta oppure
possono esistere nessi logici lettere – numeri.
Così come accade con i test costituiti da serie alfabetiche, anche la risoluzione dei
test costituiti da serie alfanumeriche si ottiene associando a ogni lettera un numero
corrispondente alla posizione della lettera nell’alfabeto.
Esempio
Completare la seguente successione, utilizzando l’alfabeto italiano: E; 95; G; 77; I; 59; ?; 41; O; ?
A. M; 44
B. L; 42
C. N; 24
D. M; 23
E. M; 20


















