
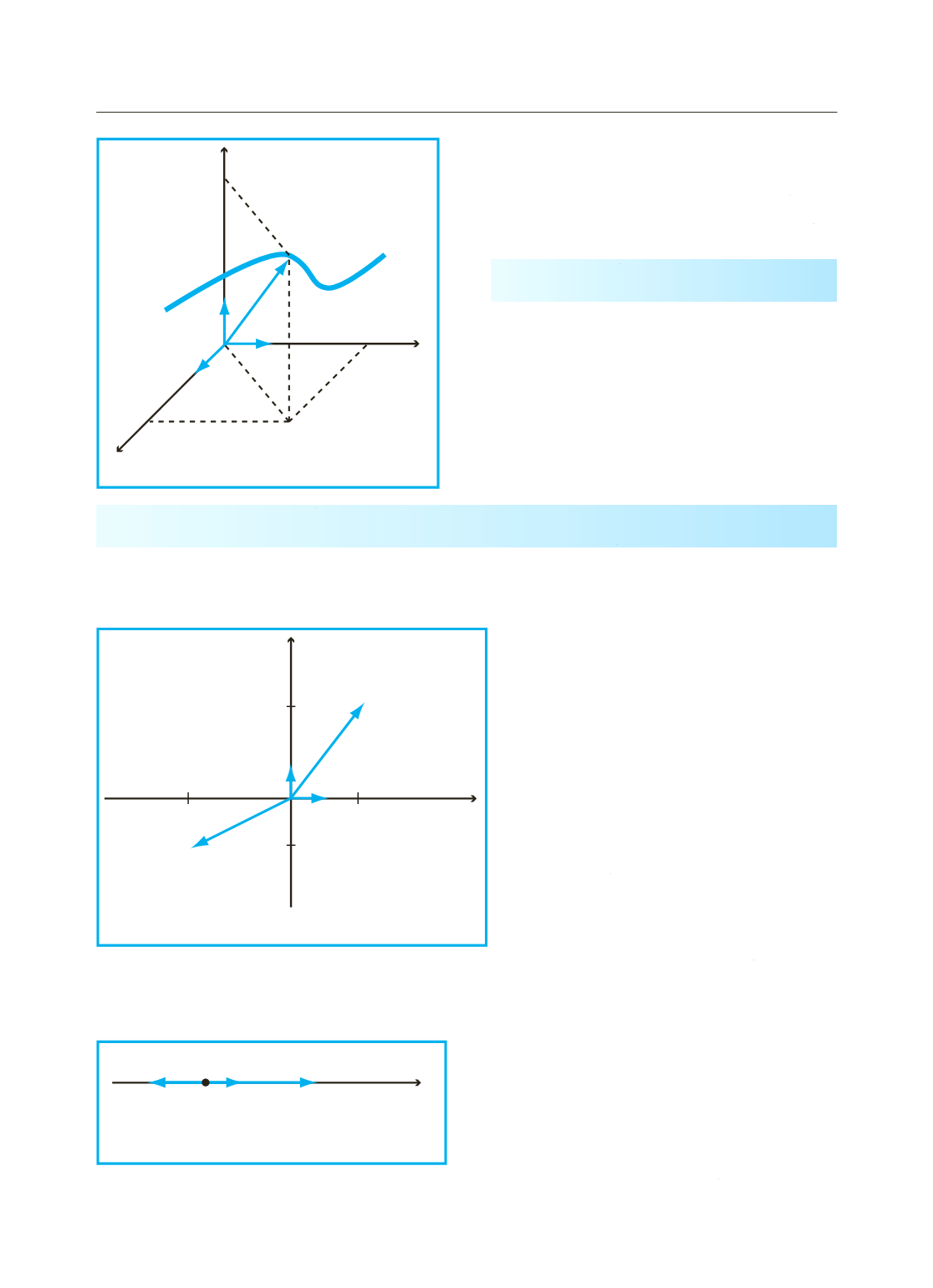
Per descrivere il moto del punto
P
è allora sufficiente conoscere in
ogni istante il raggio vettore
funzione vettoriale del tempo
o il valore delle coordinate
x
,
y
e
z
relative alla successione delle
posizioni di
P
Lo studio di un qualsiasi moto nello spazio si può pertanto ridurre
allo studio di tre moti unidimensionali.
Ad esempio, nel piano riferito
ad un sistema di assi cartesia-
ni, le posizioni di due punti
P
e
Q
sono individuate dalle
loro coordinate:
P
(3, 4)
Q
(–5, –2)
oppure dai vettori posizione:
In modo analogo sono individuate le posizioni di due punti
P
e
Q
sopra un asse, ad esempio l’asse
x
.
P
(5);
Q
(–3)
r i
r
i
P
Q
=
= −
5
3
x
5
P
O Q
–3 0 i
S
r i
j
r
i
j
P
Q
= +
= − −
3 4
5 2
O 3 i
4
Q
x
y
–5
–2
P
S
j
S
x x t y y t z z t
=
=
=
( )
( )
( )
3-2
r r t
=
( )
3-1
r
z
x
r
k
i
j
P
z
p
S
S
S
S
x
p
y
p
y
O
Generalità
61
Figura 3-2
Figura 3-3
Figura 3-4
















