
270
CAPITOLO
3
Problem Solving
www.
edises
.it
A. L’evento è impossibile
B. 1/525
C. 1/425
D. 1/235
E. 1/720
200) Un sacchetto contiene le prime dieci lettere dell’alfa-
beto italiano. Estraendo una alla volta tre lettere (senza, poi,
reintrodurle nel sacchetto) e leggendole nell’ordine di estra-
zione, qual è la probabilità che si ottenga il termine “ALA”?
A. 1/275
B. 1/525
C. L’evento è impossibile
D. 1/345
E. 1/425
201) Quale probabilità si ha di estrarre un asso da un maz-
zo di 52 carte?
A. 1/4
B. 1/13
C. 1/12
D. 1/52
E. 3/10
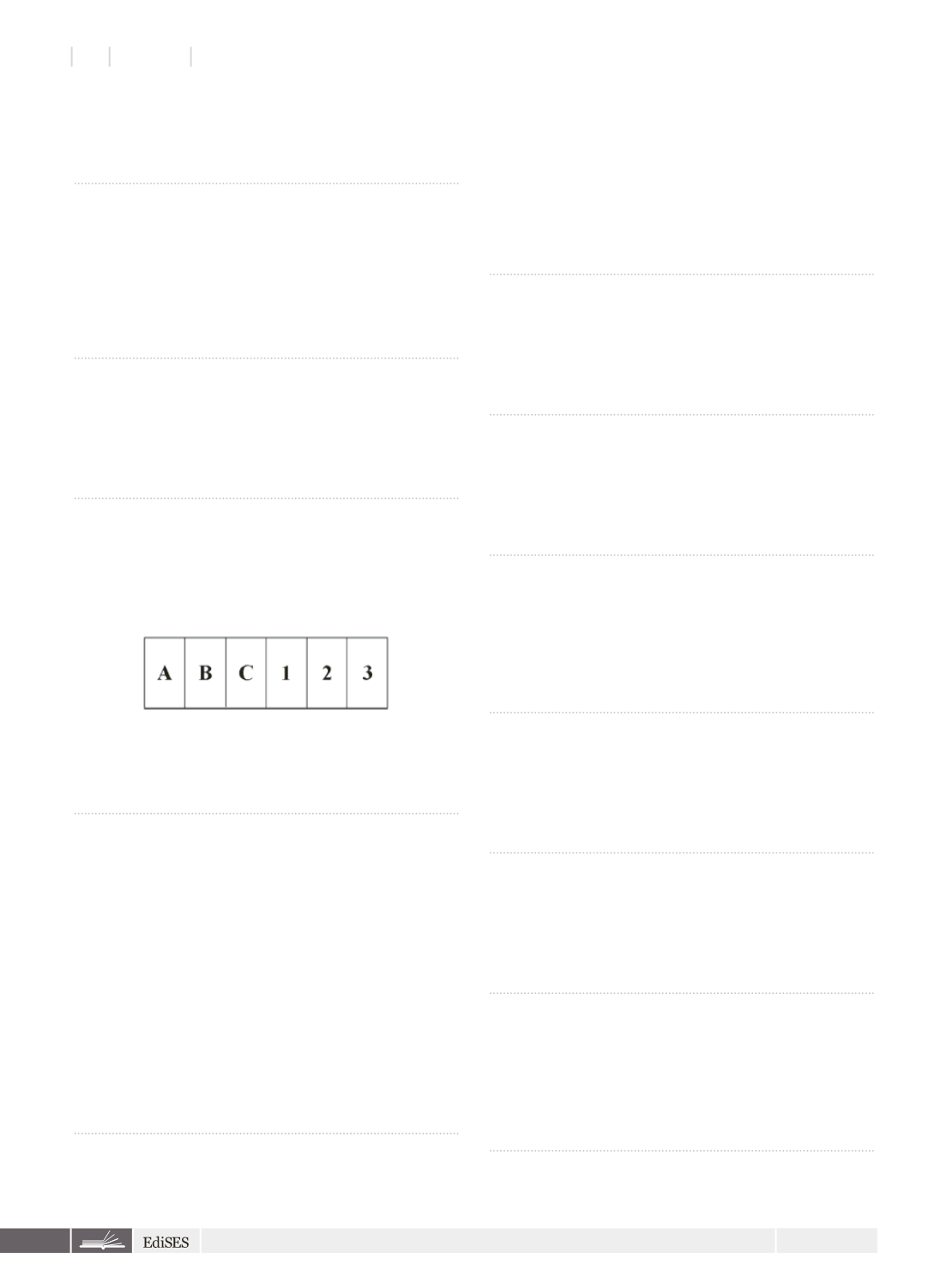
202) Prese da un mazzo particolare 6 carte, ciascuna delle
quali su un lato porta scritto una fra le lettere A, B, C e
sull’altro porta scritto una fra le cifre 1, 2, 3, Leo dispone
sul tavolo le carte come riportato sotto ed afferma:
Se una
carta porta la lettera B su un lato, sull’altro lato porta la cifra 2.
Qual è il numero minimo di carte che Maria deve girare per
essere sicura che Leo afferma il vero?
A. 4
B. 1
C. 3
D. 2
E. 6
203) Carletto ha alcune bottigliette di bibite, sui tappi delle
quali all’esterno compaiono le scritte Kuka, oppure Finta,
oppure Spruzz, mentre all’interno appare una scritta, che
dice “Hai vinto!” oppure “Non hai vinto”.
Carletto ne offre sei ad alcuni suoi amici, le stappa, guarda
i tappi sui due lati, poi posa i sei tappi sul tavolo: tre di essi
mostrano la scritta Kuka, Finta, Spruzz, mentre gli altri tre,
capovolti rispetto ai primi, mostrano le scritte “Hai vinto!”,
“Hai vinto!”, “Non hai vinto”.
Carletto afferma che chi ha bevuto Kuka ha vinto.
Qual è il minor numero di tappi che bisogna girare per ve-
rificare l’affermazione di Carletto?
A. Tre
B. Tutti e sei
C. Cinque
D. Due
E. Quattro
204) Il professor Albert, noto scienziato di fama interna-
zionale, vuole sbalordire i suoi studenti con un esperimen-
to. Egli possiede 22 palline identiche esternamente, tutte
di peso uguale tranne una che ha un peso inferiore del 10%
rispetto alle altre 21. Con una bilancia ultraprecisa con due
piatti, il professor Albert afferma che egli sarà in grado di
individuare la pallina meno pesante con sole 5 pesate e che
non è possibile farlo con un numero inferiore di pesate.
Sta affermando il vero?
A. No, sono necessarie almeno 6 pesate
B. No, sono necessarie almeno 21 pesate
C. Sì, 5 è il numero minimo di pesate necessarie
D. No, in quanto bastano al massimo 4 pesate
E. No, sono necessarie almeno 11 pesate
205) Nel lancio di un dado, qual è la probabilità che esca
un numero pari o un numero maggiore di 4?
A. 2/3
B. 3/2
C. 1/2
D. 1/4
E. 1/3
206) Quale probabilità si ha di estrarre un re da un mazzo
di 52 carte?
A. 1/52
B. 3/10
C. 1/4
D. 2/6
E. 1/13
207) Nel suo astuccio Giulia ha 1 penna blu, 2 penne nere e
3 penne rosse. Se estrae una penna a caso, qual è la proba-
bilità che essa sia nera?
A. 1/3
B. 1/5
C. 2/3
D. 1/2
E. 1/4
208) Nel gioco della tombola, qual è la probabilità che esca
alla prima estrazione 45?
A. 1/2
B. 1/90
C. 1/45
D. 1
E. 0
209) Qual è la probabilità di estrarre da un mazzo di 40
carte napoletane una carta di denari?
A. 5%
B. 1/40
C. L’evento è impossibile
D. 1/4
E. 1/10
210) Estraendo una pallina da un’urna contenente 12 palli-
ne verdi, 18 rosse e 6 nere, calcolare la probabilità che essa
sia rossa oppure nera.
A. 5/6
B. 4/5
C. 1/3
D. 3/5
E. 2/3
211) Estraendo una pallina da un’urna contenente 100 pal-
line, di cui 25 blu, 15 rosse e 60 gialle, qual è la probabilità
che esca una pallina blu?
















