
O
y
x
r
1
S
r
2
S
r
3
S
Direzione di a
v
S
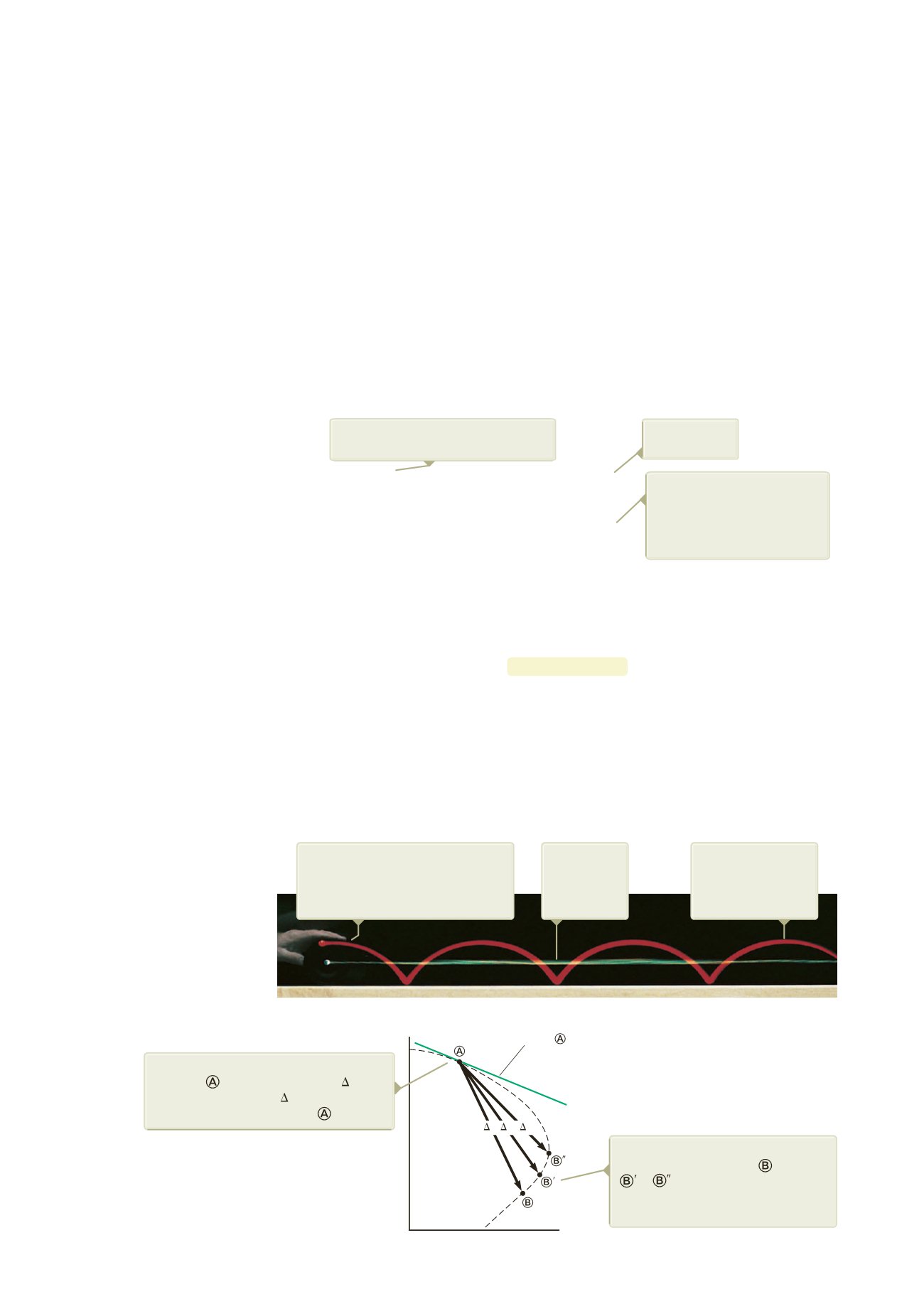
Quando l’estremo del vettore spostamento
tende ad , l’intervallo di tempo
t
tende
a zero e la direzione di tende alla linea
tangente (in verde) alla curva .
Quando l’estremo del vettore
spostamento si muove da a
a , il relativo spostamento
e gli intervalli di tempo corrispondenti
diventano sempre più piccoli.
r
S
XIV
PREFAZIONE
Problemi di impossibilità.
La ricerca sulla didattica della Fisica si è concentrata molto
sulle abilità di risoluzione dei problemi degli studenti. Benché la maggior parte dei proble-
mi di questo testo sia strutturata in una forma che fornisce dati e richiede un risultato di
calcolo, due problemi in ciascun capitolo, in media, sono strutturati come problemi di im-
possibilità. Questi sono introdotti con la frase
Perché la seguente situazione è impossibile?
, seguita
dalla descrizione di una situazione. L’aspetto sorprendente di questi problemi è il fatto che
essi non pongono alcuna domanda agli studenti oltre a quella introduttiva in corsivo. Lo stu-
dente deve determinare quali domande bisogna porsi e quali calcoli bisogna eseguire. Sulla
base dei risultati di tali calcoli, lo studente deve determinare il motivo per cui la situazione
descritta non è possibile. Tale determinazione potrebbe richiedere informazioni derivanti
da esperienze personali, buon senso, ricerche su Internet o in letteratura, misurazioni, stru-
menti matematici, conoscenza di convenzioni o pensiero scienti!co.
Questi problemi possono essere assegnati agli studenti allo scopo di far sviluppare loro
abilità di pensiero critico. Essi sono anche divertenti, avendo l’aspetto di “misteri” della !si-
ca che gli studenti, individualmente o in gruppo, devono risolvere. Un esempio di problema
di impossibilità è riportato di seguito:
51.
Perché la seguente situazione è impossibile?
Albert Pujols
scaglia un fuori campo che va
a s!orare la !la più alta
delle gradinate, a 24.0 m di altezza e a 130 m dal punto
di battuta. La velocità impressa alla palla è 41.7 m/s a
un angolo di
35.0° rispetto all’orizzontale. La resisten-
za dell’aria è trascurabile.
La domanda iniziale in corsivo designa
un problema di impossibilità.
Viene descritta
la situazione.
Non viene posto alcun quesito.
Lo studente deve determinare
ciò che è necessario per il
calcolo e il motivo per il quale
la situazione è impossibile.
Incremento del numero di problemi accoppiati.
In seguito al riscontro positivo ottenu-
to da una ricerca di mercato, abbiamo aggiunto altri problemi accoppiati in questa edizione.
Si tratta di problemi identici, ma uno richiede una soluzione numerica e l’altro una deriva-
zione simbolica. In questa edizione, sono presenti tre coppie di tali problemi alla !ne della
maggior parte dei capitoli, indicati da un’ombreggiatura.
Estensiva revisione della gra7ca.
Ogni elemento iconogra!co della Quinta edizione è pre-
sentato in uno stile moderno che contribuisce a esprimere i principi di Fisica in azione in modo
chiaro e preciso. Ciascun elemento iconogra!co è stato inoltre revisionato in modo tale da garan-
tire che la situazione !sica presentata corrisponda esattamente alla discussione in esame.
In molte !gure sono inclusi
fumetti esplicativi
, che sottolineano aspetti importanti della !-
gura o guidano gli studenti attraverso un processo illustrato dalla !gura o dalla foto. Questo
formato aiuta gli studenti che hanno un tipo di apprendimento più visivo. Esempi di !gure
con fumetti esplicativi sono riportati di seguito.
Henry Leap and Jim Lehman
Una sorgente di luce al centro di un
cilindro in rotazione e un’altra in un
punto sul bordo illustrano i differenti
percorsi che questi due punti compiono.
Il punto sul bordo si
muove su un percorso
denominato cicloide
(linea rossa).
Il centro si
muove su una
linea retta
(linea verde).
Figura 34.67
Due punti su un
oggetto che rotola percorrono
diversi cammini nello spazio.
Figura '.)
Quando una particella si muove tra due
punti, la sua velocità media ha la direzione del vettore
spostamento
D
S
r
. Per de"nizione, la velocità istantanea
in
A
è diretta lungo la linea tangente in
A
alla curva.
















