
PREFAZIONE
XI
Esempio
|
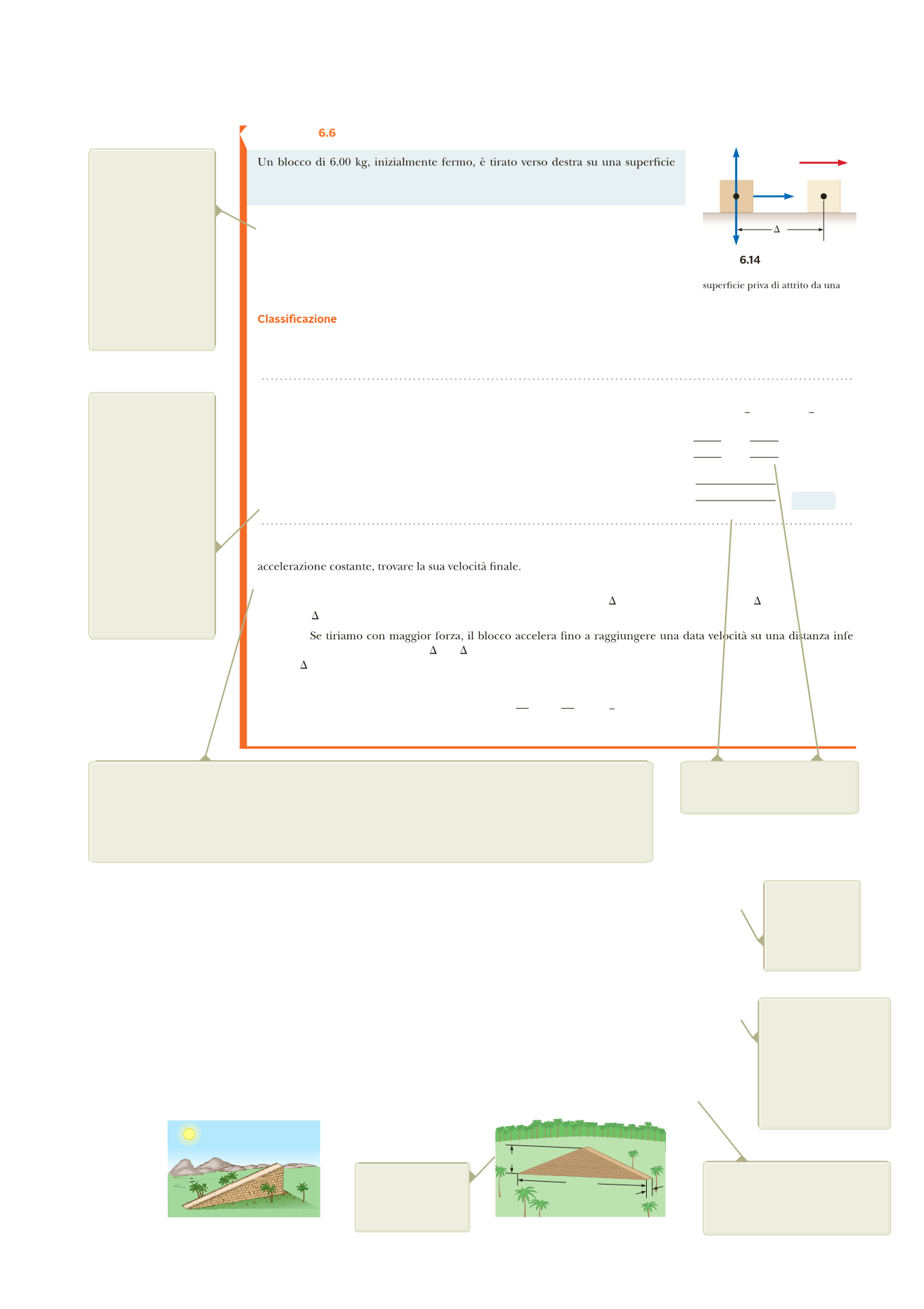
Un blocco trascinato su una superficie senza attrito
orizzontale liscia da una forza costante orizzontale di 12.0 N. Trovare la velocità del
blocco dopo che si è spostato di 3.00 m.
SOLUZIONE
Concettualizzazione
La Figura 6.14 illustra la situazione. Immagina di tirare un’au-
tomobile giocattolo su un tavolo orizzontale con un elastico orizzontale attaccato
alla parte anteriore dell’auto. La forza viene mantenuta costante assicurandosi che
l’elastico allungato abbia sempre la stessa lunghezza.
Potremmo applicare le equazioni della cinematica per determinare la soluzione, ma scegliamo di
utilizzare l’approccio mediante considerazioni energetiche. Il blocco è il sistema, e tre forze esterne interagiscono con
esso. La forza normale bilancia la forza di gravità sul blocco. Né la forza di gravità né la forza normale compiono lavoro
sul blocco perché queste forze sono verticali e lo spostamento è orizzontale.
Analisi
La forza esterna risultante sul blocco è la forza orizzontale di 12 N.
Usando il teorema dell’energia cinetica e notando che l’energia cinetica
iniziale è zero, troviamo:
Risolviamo rispetto a
v
f
ed usiamo l’Equazione 6.1 per il lavoro svolto sul
blocco da
F
:
:
Sostituisci i valori numerici:
Conclusione
Ti sarebbe utile risolvere questo problema di nuovo descrivendo il blocco come una particella sotto l’azio-
ne di una forza risultante per determinarne l’accelerazione e quindi, trattandola come una particella che si muove con
E se…?
Supponiamo che il modulo della forza in questo esempio venga raddoppiato a
F
v
5
2
F
. Il blocco di 6.0 kg ac-
celera a 3.5 m/s a causa della forza applicata durante lo spostamento
x
v
. Come è lo spostamento
x
v
rispetto a quello
originario
x
?
Risposta
-
riore, pertanto ci aspettiamo che
x
v
<
x
. In entrambi i casi, il blocco sperimenta lo stesso cambiamento di energia
cinetica
K
. Matematicamente, dal teorema dell’energia cinetica troviamo:
W
est
5
F
9D
x
95 D
K
5
F
D
x
D
x
95
F
F
9
D
x
5
F
2
F
D
x
5
1
2
D
x
e la distanza è inferiore, come suggerito dal nostro ragionamento.
x
f
v
S
F
S
m
g
S
n
S
Figura
(Esempio 6.6) Un
blocco tirato verso destra su una
forza costante.
W
est
5
K
f
2
K
i
5
1
2
mv
f
2
2
0
5
1
2
mv
f
2
v
f
5
Å
2
W
est
m
5
Å
2
F
D
x
m
v
f
5
Å
2(12 N)(3.0 m)
6.0 kg
5
3.5 m/s
Gli incisi
“E se?”
sono presenti in circa un terzo degli esempi svolti e presentano una variante della
situazione descritta nel testo dell’esempio. Ad esempio, un tale elemento potrebbe esplorare gli
effetti di una variazione delle condizioni iniziali, determinare cosa accade quando una grandezza
viene assunta a un certo valore limite, o chiedere se possano essere determinate informazioni
aggiuntive relative al problema. Questo elemento incoraggia gli studenti a riflettere sui risultati
dell’esempio e assiste nella comprensione concettuale dei principi.
Il risultato finale è simbolico;
i valori numerici vengono
sostituiti nel risultato finale.
Ciascun passaggio
della soluzione
è presentato in
un formato a
due colonne. La
colonna di sinistra
fornisce una
spiegazione di
ogni passaggio
matematico
presente nella
colonna di destra,
in modo da
consolidare meglio
i concetti di Fisica.
Ogni soluzione è
stata scritta in
modo da seguire
fedelmente la
Strategia per la
risoluzione dei
problemi presentata
nel Capitolo 1, in
modo tale da
rafforzare la
capacità di risolu-
zione dei problemi.
Viene fornita
una breve
introduzione
riguardo al
problema.
Il calcolo richiesto
viene reso più perso-
nale richiedendo la
stima del lavoro fatto
dagli uomini piutto-
sto che il calcolo
dell’energia poten-
ziale gravitazionale.
L’espressione per l’energia
potenziale gravitazionale viene
fornita, mentre inizialmente
veniva richiesto di dimostrarla.
Problema dalla Quarta Edizione…
35.
(a) Consideriamo un corpo esteso le cui dif-
ferenti parti si trovano a differenti altezze.
Assumere che l’accelerazione di caduta libe-
ra sia uniforme su tutto il corpo. Provare che
l’energia potenziale gravitazionale del sistema
corpo-Terra è data da
U
g
5
Mgy
CM
, dove
M
è
la massa totale del corpo e
y
CM
è l’altezza del
centro di massa rispetto al livello di riferimen-
to scelto. (b) Calcolare l’energia potenziale
gravitazionale associata a una rampa costruita
rispetto al suolo con pietre di densità 3 800
kg/m
3
e larga 3.60 m (Fig. P8.35). Vista di lato
la rampa è un triangolo rettangolo di altezza
15.7 m e base 64.8 m.
Figura P(.*+
…Come revisionato nella Quinta Edizione:
37.
Degli esploratori trovano nella giungla un antico mo-
numento della forma di un grande triangolo isoscele
come mostrato in Figura P8.37. Il monumento è for-
mato da migliaia di piccoli blocchi di pietra di densità
3 800 kg/m
3
. Il monumento è alto 15.7 m e largo 64.8
m alla base, con uno spessore uniforme di 3.60 m. Pri-
ma della costruzione del monumento, i blocchi di pie-
tra giacevano al suolo. Quanto lavoro hanno compiuto
i lavoratori sui blocchi nel portarli nella loro posizio-
ne attuale, quando hanno costruito il monumento?
Nota
: l’energia potenziale gravitazionale di un sistema
oggetto-Terra è data da:
U
g
5
Mgy
CM
, dove
M
è la massa
totale dell’oggetto e
y
CM
l’altezza del centro di massa al
di sopra del livello di riferimento scelto.
3.60 m
64.8 m
15.7 m
Figura P(.*,
La $gura è stata
revisionata e sono
state aggiunte le
dimensioni.
















