16.2
■
Significato geometrico della derivata
299
Supponiamo ora che
f
sia derivabile in
x
o
e sia
f
′
(
x
0
) la sua derivata:
f
′
(
x
0
)
=
lim
x
S
x
0
f
(
x
)
–
f
(
x
0
)
––––––––––––
x
–
x
0
Indichiamo in!ne con
s
0
la retta di equazione:
y
–
f
(
x
0
)
=
f
′
(
x
0
)(
t
–
x
0
),
ove
t
varia in
R
.
Se
x
tende verso
x
0
, allora
f
(
x
) tende verso
f
(
x
0
), grazie alla continuità
di
f
in
x
0
e il punto
Q
di coordinate
(
x
,
f
(
x
)
)
“tende” al punto
P
di coordi-
nate
(
x
0
,
f
(
x
0
)
)
.
D’altra parte, se
x
tende verso
x
0
, allora:
f
(
x
)
–
f
(
x
0
)
––––––––––––
x
–
x
0
tende verso
f
′
(
x
0
)
e cioè
il coef!ciente angolare della retta secante s
(
x
)
tende al coef!ciente angolare
f
′
(
x
0
)
della retta s
0
.
Perciò è del tutto naturale chiamare la retta
s
0
retta tangente
al gra!co di
f
nel punto
(
x
0
,
f
(
x
0
)
)
.
Il signi!cato geometrico
della derivata
f
′
(
x
0
) è dunque quello di
coef!ciente
angolare
(o
pendenza
)
della tangente
al gra!co di
f
in
(
x
0
,
f
(
x
0
)
)
.
Osservazione 16.5.
Se la derivata di
f
in
x
0
è uguale a zero:
f
′
(
x
0
)
=
0,
allora, il coef!ciente angolare della tangente è uguale a zero e la tangente
al gra!co nel punto
(
x
0
,
f
(
x
0
)
)
è parallela all’asse
x
(Figura 16.2).
\
I [
I [
[
V
V [
[
3
4
W
\
[
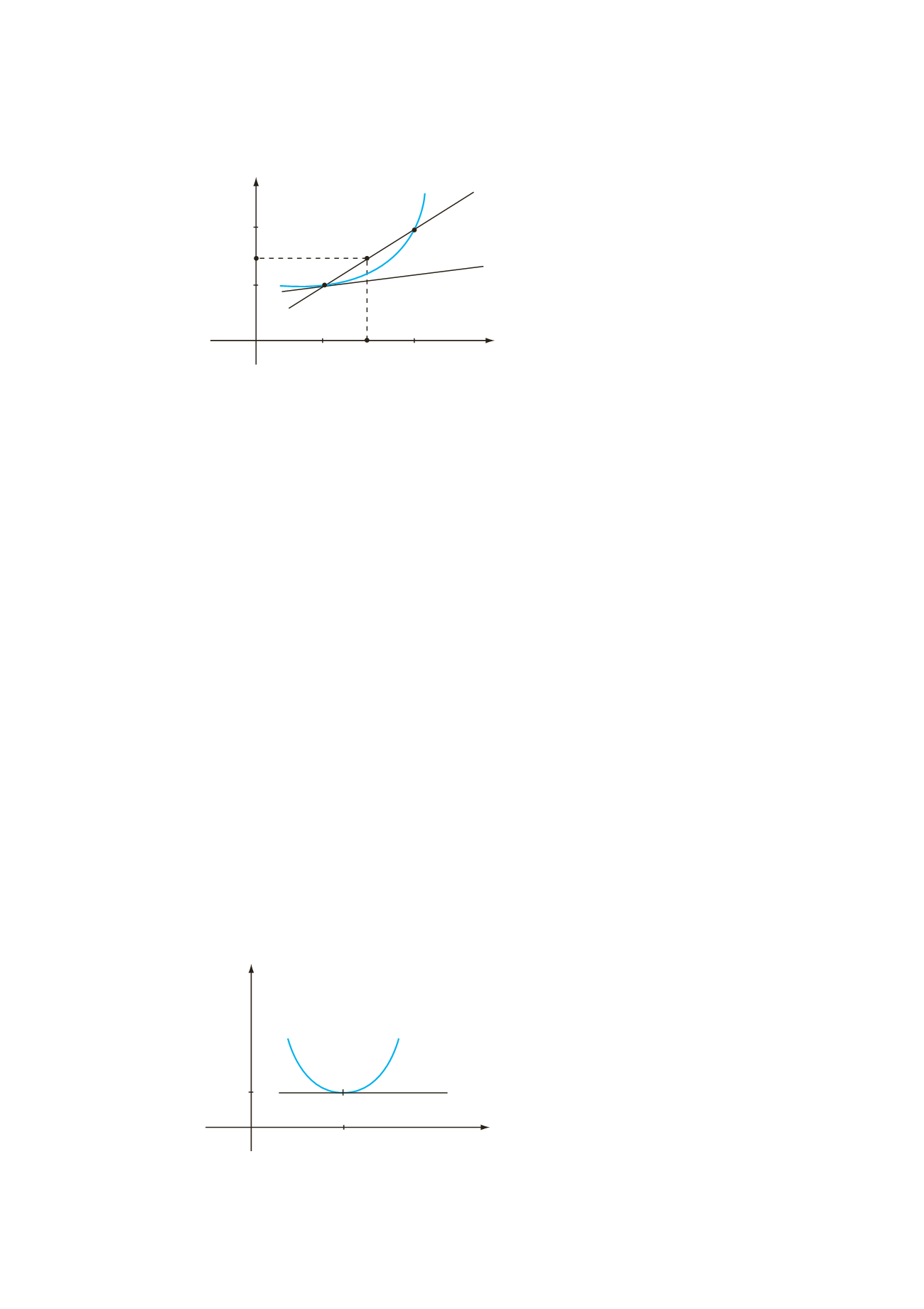
FIGURA 16.1
\
I [
I [
[
[
FIGURA 16.2


