
CAPITOLO
2
Ragionamento critico
41
www.
edises
.it
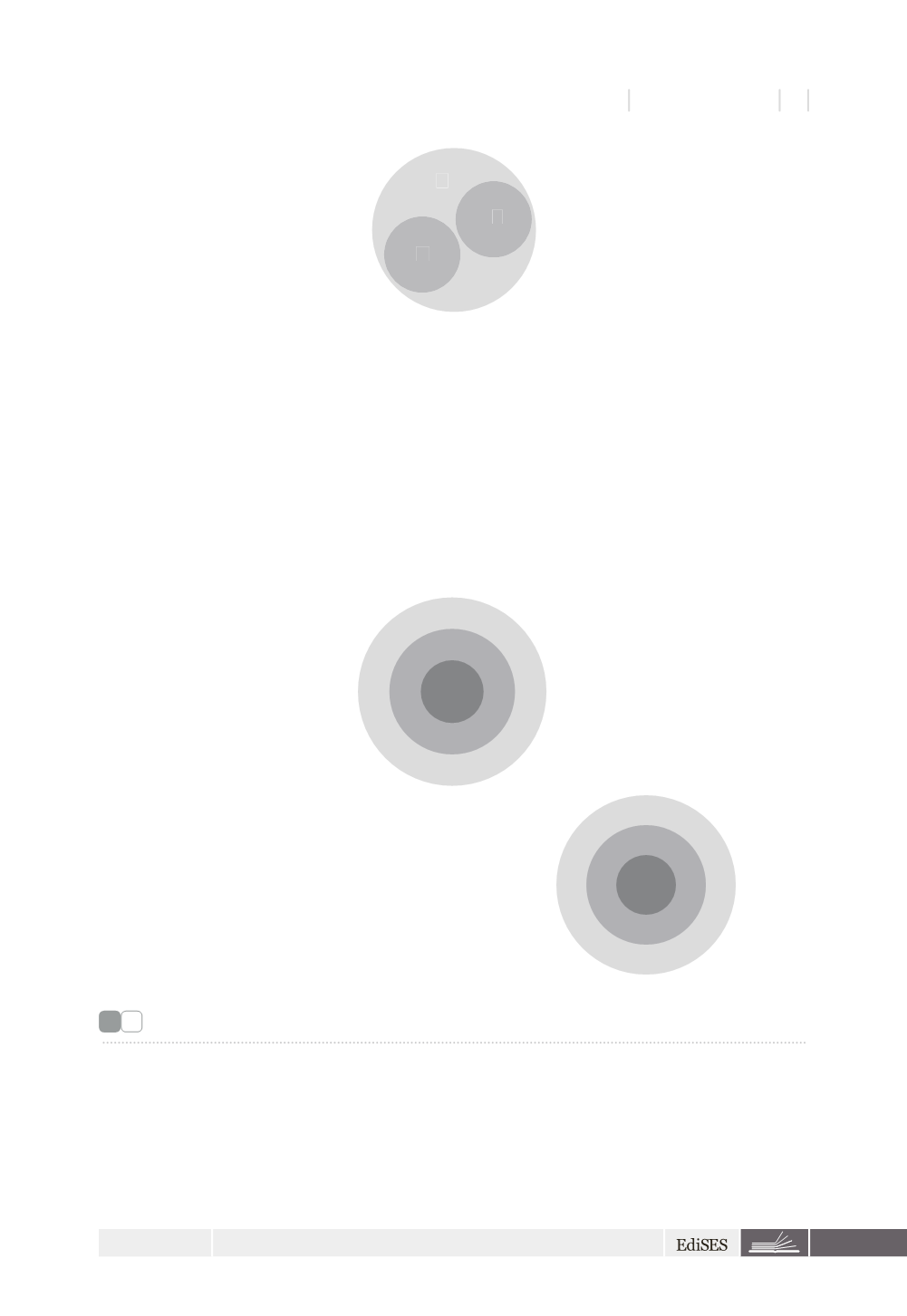
B
C
A
L’insieme C può contenere i due sottoinsiemi A e B che tuttavia mantengono la loro
reciproca autonomia. Per riportare l’esempio in un contesto concreto si pensi al rap-
porto tra stoviglie, piatti e bicchieri. Tutti i piatti (A) rientrano nell’insieme stoviglie
(C); tutti i bicchieri (B) rientrano nell’insieme stoviglie (C) ma non c’è alcuna so-
vrapposizione tra i due insiemi B e A.
Se invece il sillogismo fosse stato:
Tutti gli A sono B (oppure tutti i milanesi sono lombardi)
Tutti i B sono C (oppure tutti i lombardi sono italiani)
Quindi tutti gli A sono C (quindi tutti i milanesi sono italiani)
le conclusioni sarebbero da considerare accettabili?
Dalla figura sottostante si capisce immediatamente la risposta
B
C
A
Tutti i
B
sono
C
Tutti gli
A
sono
B
{
{
C
A
È corretto concludere che
➝
Tutti gli A sono C
➝
2.1.1
•
Come aiutarsi con i diagrammi insiemistici
Esistono tre tipi di relazioni che possono intercorrere fra due o più insiemi, e cioè:
INCLUSIONE
: si ha quando
TUTTI
gli elementi di un insieme sono anche elementi
di un secondo insieme.


















