
Capitolo
2
Lo stato solido e lo stato gassoso
39
www.
edises
.it
c
a
A B
g
b
a
D
F
C
G L
b
H
a
b
c
E
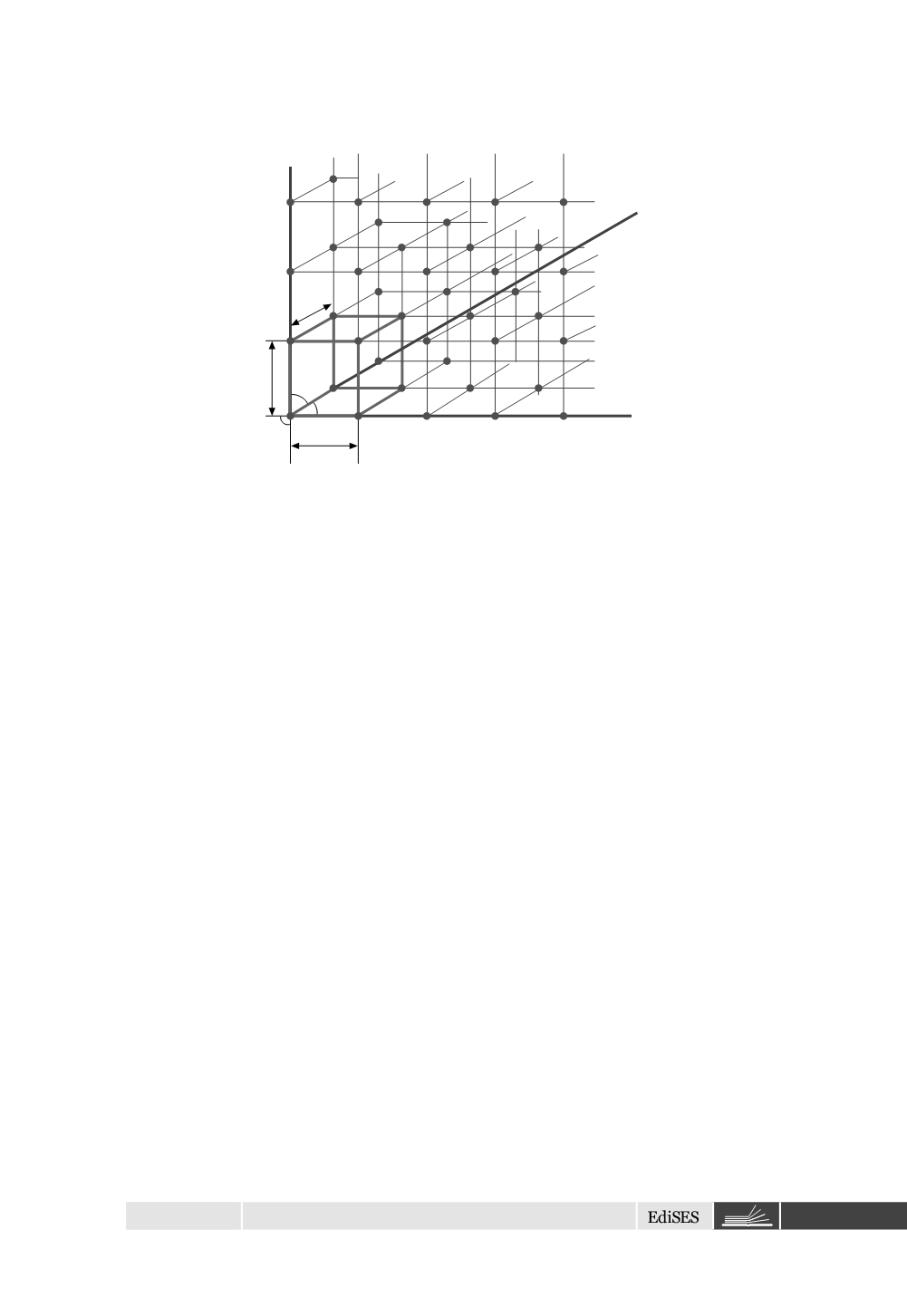
Figura 2.2
Rappresentazione di punti a tre dimensioni: reticolo tridimensionale.
a
è
l’angolo formato tra gli assi
a
e
b
,
b
l’angolo tra
b
e
c
,
g
l’angolo tra
a
e
c
.
2.3
Sistemi cristallini
Esistono solo
sette
diversi tipi di celle elementari alle quali corrispondono
set-
te
sistemi
cristallini
. In Figura 2.3 sono riportate le celle elementari dei sette
sistemi cristallini.
Se mettiamo un punto reticolare in ogni angolo della cella elementare,
otteniamo una
cella
primitiva
. Tutti i sette reticoli in Figura 2.3 sono reticoli
primitivi.
È anche possibile generare quelli che vengono chiamati
reticoli
centrati
posi-
zionando un punto reticolare in posizioni specifiche nella cella elementare.
Questo viene illustrato per un reticolo cubico in Figura 2.4. Un
reticolo
cubico
a
corpo
centrato
possiede un punto reticolare al centro della cella elementare
in aggiunta ai punti reticolari agli otto angoli. Un
reticolo
cubico
a
facce
cen-
trate
ha un solo punto reticolare al centro di ciascuna delle sei facce della cella
elementare in aggiunta ai punti reticolari agli otto angoli. I reticoli centrati
esistono anche per altri tipi di celle elementari.
2.4
Il riempimento di una cella elementare
Il reticolo di per sé non definisce la struttura di un cristallo. Per generare una
struttura cristallina, dobbiamo associare un atomo o un gruppo di atomi ad
ogni punto del reticolo.
Nel caso più semplice, la struttura del cristallo consiste di atomi identici, ed
ogni atomo giace direttamente su un punto reticolare. Si tenga a mente che
solo
gli
elementi
possono formare strutture di questo tipo. Per i composti, anche
se mettessimo un atomo in ogni punto reticolare, i punti non sarebbero iden-
tici in quanto gli atomi non sono tutti uguali.
















