
38
Scienze e tecnologie chimiche
000
www.
edises
.it
con la convenzione che tutti gli altri punti si trovino in posizioni individuate da
altri numeri interi, –1, 2, 3 ecc. Nel caso in cui al posto dei punti si abbiano del-
le particelle, la disposizione di questo filare di particelle viene chiamata
reticolo
ad
una dimensione
. In esso una coppia di numeri individua due particelle che
corrispondono alla cosiddetta
cella elementare
(o
unitaria
)
ad una dimensione
.
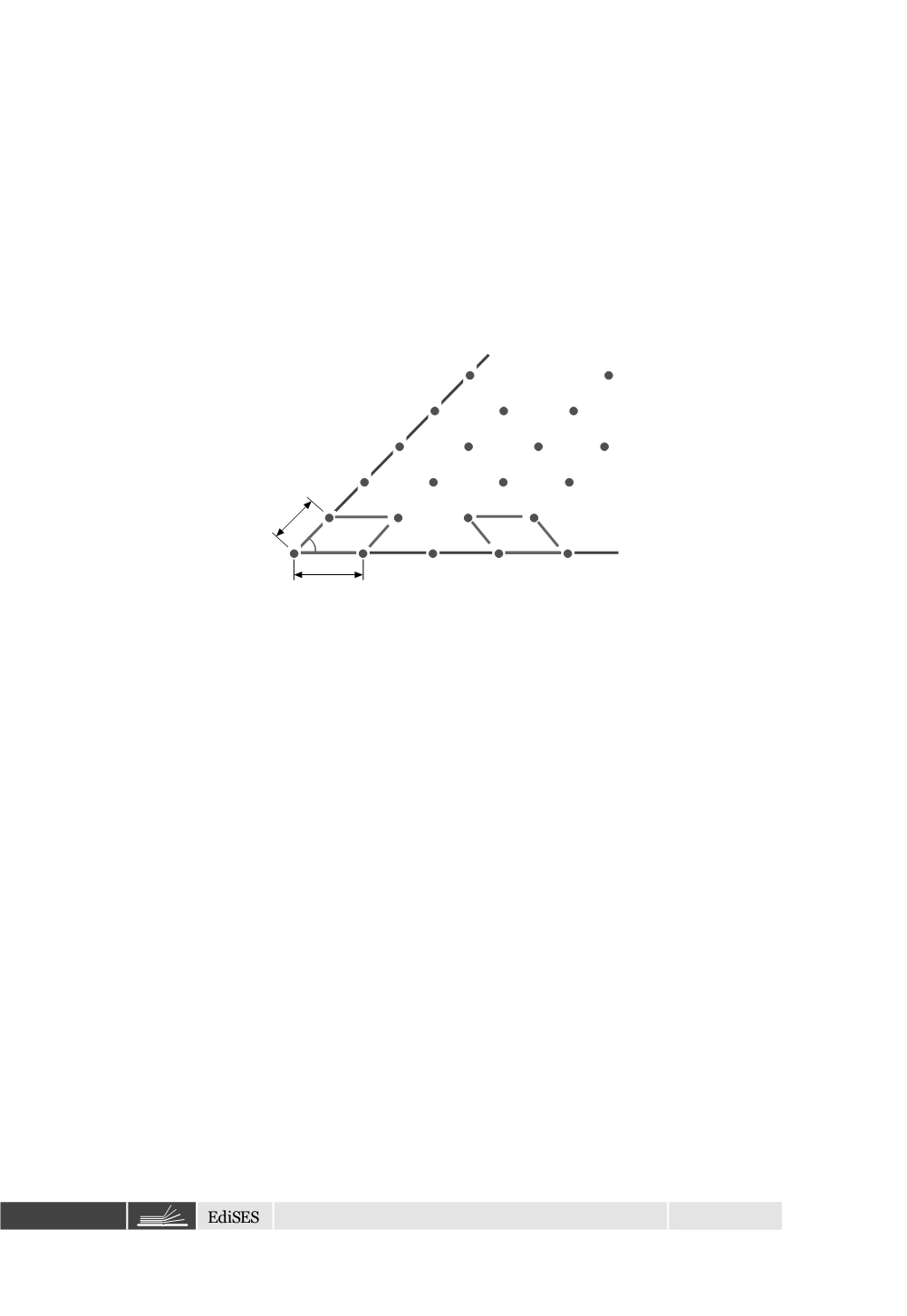
Se ora vogliamo descrivere una serie ordinata di punti o di particelle disposti
in due dimensioni, cioè in un piano, bisogna utilizzare due rette
a
e
b,
che pos-
sono essere considerate come assi
x
e
y
, e l’angolo
a
tra di esse (vedi Figura 2.1).
A
D
C H
G
b
a
B
E
F
a
b
a
Figura 2.1
Rappresentazione di punti a due dimensioni: reticolo a due dimensioni.
Le distanze costanti tra i punti disposti su queste rette vengono chiamate
a
e
b
e l’insieme dei punti ABCD rappresenta la
cella
elementare
a
due
dimen-
sioni
. In base alle coordinate scelte, il punto E è individuato dalla coppia di
numeri (3,0), il punto F da (4,0), il punto G da (3,1) e il punto H da (2,1).
La ripetizione della cella elementare a due dimensioni costituisce un
reticolo
a due dimensioni
.
Se si vuole rappresentare una serie ordinata di punti in tre dimensioni biso-
gna utilizzare tre rette
a
,
b
e
c
, che possono essere considerate come assi
x
,
y
,
z
(che non sono necessariamente assi cartesiani ortogonali), e gli angoli
a
,
b
e
g
formati tra di esse (vedi Figura 2.2).
Le distanze costanti tra i punti disposti su queste rette vengono chiamate
a
,
b
e
c
ed un insieme di otto punti, ABCDEFGH, individua la
cella
elementare
a
tre
dimensioni
. Il
reticolo
cristallino
si può immaginare quindi formato dalla
ripetizione regolare lungo tre direzioni della cella elementare a tre dimensio-
ni, che rappresenta la sua unità costitutiva fondamentale e che ha sempre la
forma di un parallelepipedo. I cristalli di una stessa specie cristallina, inoltre,
hanno costanti gli angoli diedri formati dalle superfici piane che delimitano il
cristallo: tali superfici vengono chiamate
facce
.
Nell’esempio riportato in Figura 2.2,
a
=
b
=
g
= 90° e a = b = c. Allora la figura
geometrica ottenuta individua un cubo che rappresenta il più semplice e simme-
trico insieme di punti che, ripetuto nelle tre dimensioni, riproduce la disposizio-
ne geometrica del solido cristallino. Questi punti che rappresentano le posizioni
occupate dalle particelle del solido sono detti
punti
o
nodi
o
siti
reticolari
.
















