
IGIENE, EPIDEMIOLOGIA E MEDICINA PREVENTIVA
6
1.2 Analisi di variabili quantitative
Le variabili quantitative possono essere continue (es. peso od altezza) o discrete (es. giorni di degenza). Per essere
descritte si utilizzano misure di centralità e di dispersione
1.2.1
MISURE DI CENTRALITÀ
¾
Moda
: valore più frequente in una data distribuzione di frequenze
¾
Media
: sommatoria dei valori/numero dei valori:
X
=
i
=
1
n
X
i
n
®
È “influenzata” dai cosidetti
outliers
, ovvero valori anomali o aberranti che si discostano chiaramente dalle altre
osservazioni
¾
Mediana
: valore che divide in due parti uguali una serie ordinata (in senso ascendente o discendente)
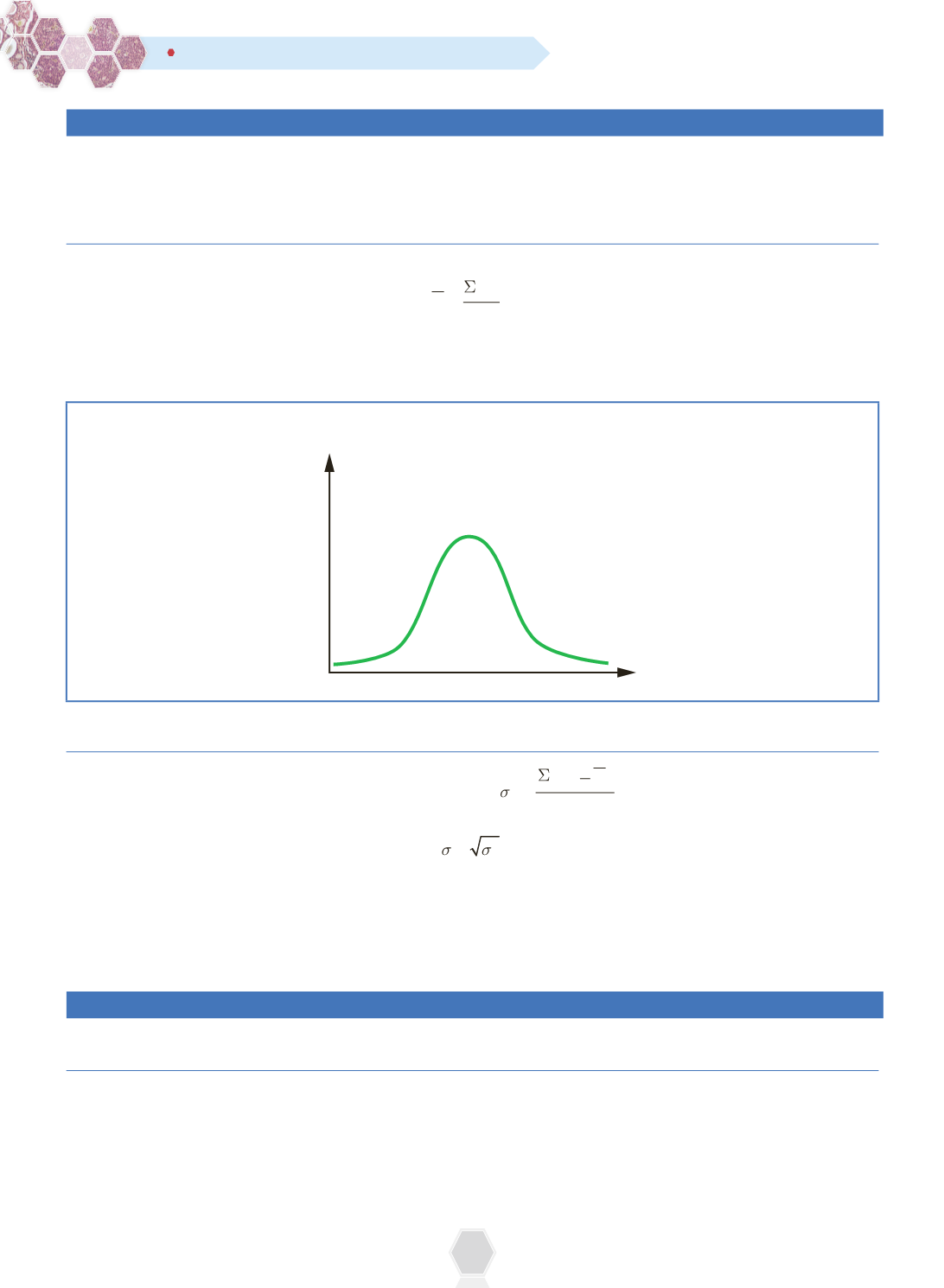
Esempio
In una distribuzione normale o gaussiana, media = moda = mediana
0HGLD 0RGD 0HGLDQD
)UHTXHQ]D
9DORUL
1.2.2
MISURE DI DISPERSIONE
¾
Devianza
: sommatoria degli scarti dalla media al quadrato:
2
=
X
i
X
(
)
2
n
i
=
1
n
¾
Deviazione standard
: dispersione dei dati attorno al valore atteso
®
Corrisponde alla radice quadrata della varianza:
=
2
®
In una gaussiana, l’intervallo media +- DS comprende circa il 68% dei valori, media +- 2DS il 96% e media +- 3DS
il 99,7%
¾
Intervallo interquartile
: differenza tra il 3° e il 1° quartile (rispettivamente il 75% e il 25% dei valori), contiene il
50% dei valori
®
Viene usato insieme alla mediana nelle distribuzioni non gaussiane
1.3 Fattori causali e fattori di rischio
1.3.1
FATTORI CAUSALI
Sono fattori che provocano la malattia
¾
Possono essere:
®
Necessari e sufficienti
, quando vi è un rapporto biunivoco tra causa ed effetto, ovvero se c’è la malattia significa
che c’è stato il fattore causale e viceversa, se c’è il fattore causale si svilupperà necessariamente la malattia
®
Necessari ma non sufficienti
, quando il fattore è necessario a determinare una determinata patologia ma di per sé
non sufficiente (es. malattie infettive)
















