
www.
edises
.it
Capitolo 4
Ragionamento numerico
213
Date una grandezza
A
, che assume valori
a
e
a
l
, e una grandezza
B
, direttamente pro-
porzionale ad
A
, che, in corrispondenza di tali valori di
A
, assume valori
b
e
b
l
:
A B
a
"
b
a
l
"
b
l
In tal caso, potremo scrivere la proporzione:
a
:
a
l
=
b
:
b
l
&
a
:
b
=
a
l
:
b
l
(nell’ultimo passaggio abbiamo scambiato i medi).
In un problema del “tre semplice” diretto abbiamo due grandezze
A
e
B
che sono
direttamente proporzionali. Vengono forniti due valori per la grandezza
B
(ad
esempio
b
e
b
l
) e un valore per la grandezza
A
(ad esempio
a
, corrispondente al
valore
b
di
B
). Si chiede di fornire il valore incognito
x
della grandezza
A
corrispon-
dente al valore
b
l
di
B
.
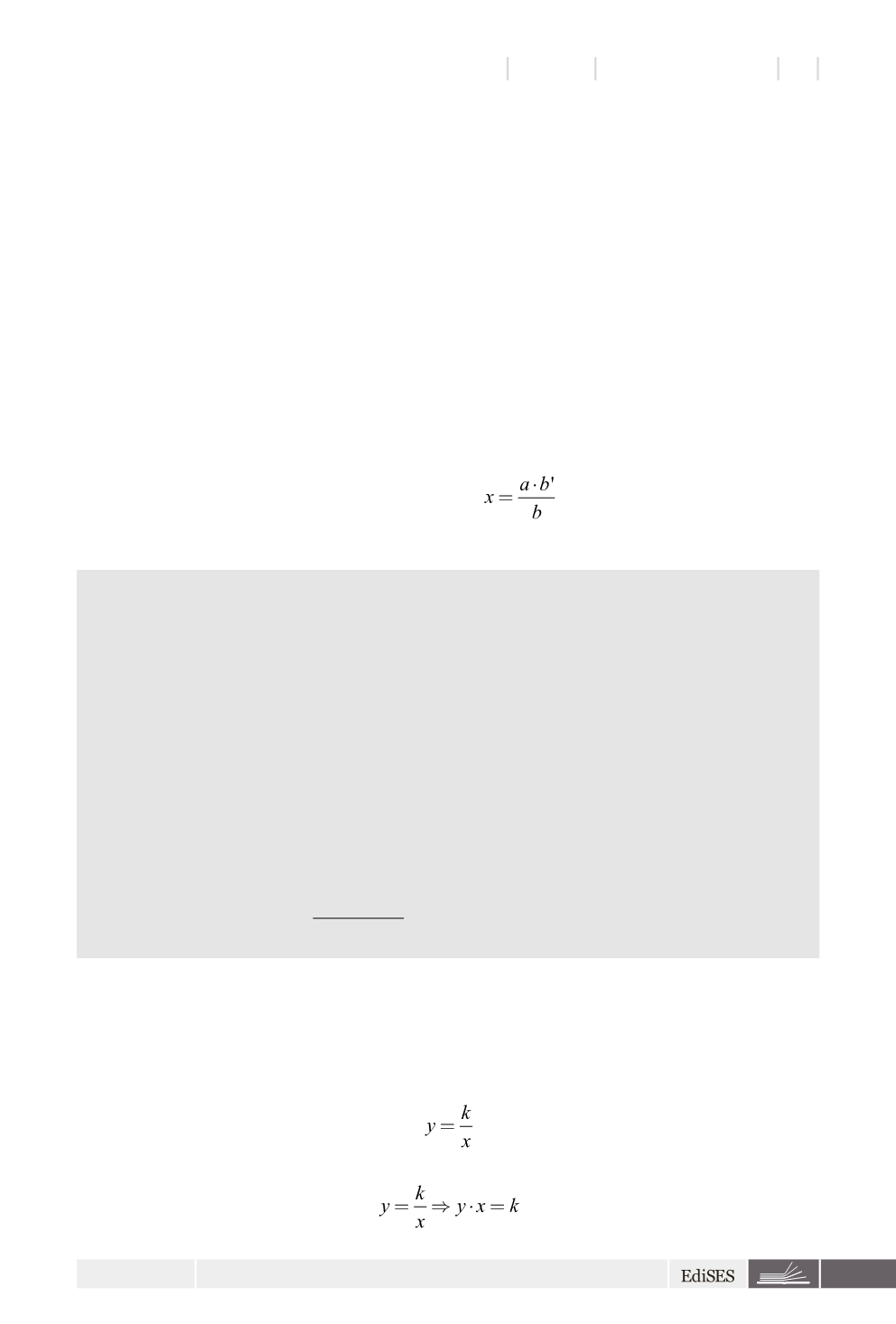
Si può quindi impostare la proporzione e risolverla:
a
:
x
=
b
:
b
l
&
Analizziamo un quesito della banca dati sulla proporzionalità diretta.
Esempio
In una casa editrice, 34 redattori correggono 1.768 pagine di bozza al giorno. Lavorando allo
stesso ritmo, quante pagine saranno corrette al giorno da 60 redattori?
A. 3.300
B. 3.090
C. 3.450
D. 3.060
E. 3.120
La risposta esatta è
E
.
Il numero di redattori e le pagine corrette sono due grandezze direttamente proporzionali: all’au-
mentare dei redattori aumentano le pagine di bozza.
Impostiamo, quindi, la proporzione:
34 redattori : 60 redattori = 1.768 pagine :
x
pagine
da cui:
x
=
60 redattori
34 redattori
⋅
1.768 pagine
=
3.120
pagine
Proporzionalità inversa e “tre semplice”
Due grandezze variabili e tra di loro dipendenti sono inversamente proporzionali
quando al raddoppiare, triplicare ecc. di una, il corrispondente valore dell’altra di-
venta la metà, un terzo ecc.
Se
x
e
y
sono inversamente proporzionali e
k
è una costante, allora possiamo scrivere:
Da questo si evince che il prodotto tra
x
e
y
è costante:


















