
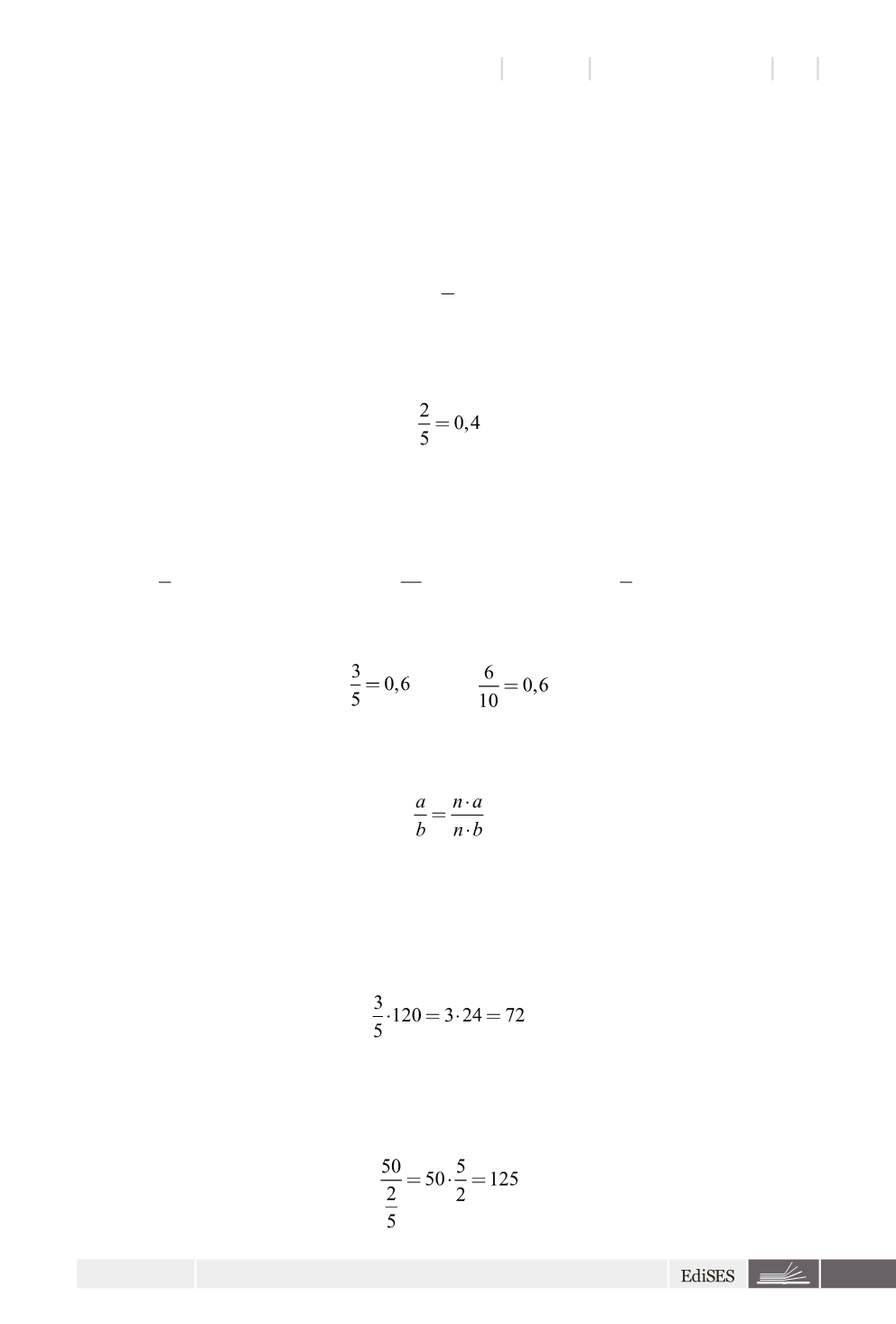
www.
edises
.it
Capitolo 4
Ragionamento numerico
209
Di seguito, per ciascuna tipologia, esponiamo alcune regole utili per la risoluzione,
nonché esempi tratti dalla banca dati.
4.4.1
Frazioni
Una frazione è una coppia ordinata di numeri (
a
,
b
) con
b
non nullo che assume il
valore numerico
a
:
b
ed è indicata con:
a
b
a
è detto
numeratore
e
b
è detto
denominatore
.
Le frazioni si possono ovviamente esprimere in termini di numeri decimali se calco-
liamo la divisione tra numeratore e denominatore:
2/5 è detta frazione generatrice di 0,4.
Una frazione si dice
propria
se il numeratore è minore del denominatore,
impropria
se
il numeratore è maggiore del denominatore e
apparente
se il numeratore è multiplo
del denominatore.
Propria:
3
7
Impropria:
10
3
Apparente:
8
2
Due frazioni si dicono
equivalenti
se assumono lo stesso valore, cioè se sono frazioni
generatrici dello stesso numero:
Da questo si deduce che data una frazione è possibile ricavarne una equivalente
moltiplicando o dividendo numeratore e denominatore per lo stesso numero
n
, ad
esempio:
Una frazione si dice
ridotta ai minimi termini
se il massimo comun divisore (MCD) tra
numeratore e denominatore è 1 (numeri primi tra loro).
Data una certa quantità
x
, se ne può calcolare la parte frazionaria, moltiplicando la
frazione per la quantità stessa.
Ad esempio, se la quantità è
x
= 120 e vogliamo calcolarne i 3/5, allora la parte fra-
zionaria incognita è:
Talvolta, è nota la parte frazionaria e se ne vuole calcolare la quantità
x
. In tale caso,
occorre dividere la parte per la frazione.
Ad esempio, se la parte frazionaria di un numero è 50 e tale parte corrisponde ai 2/5
di un numero, allora il numero incognito è:


















