
Soluzioni
- Logica numerica
385
6)
D.
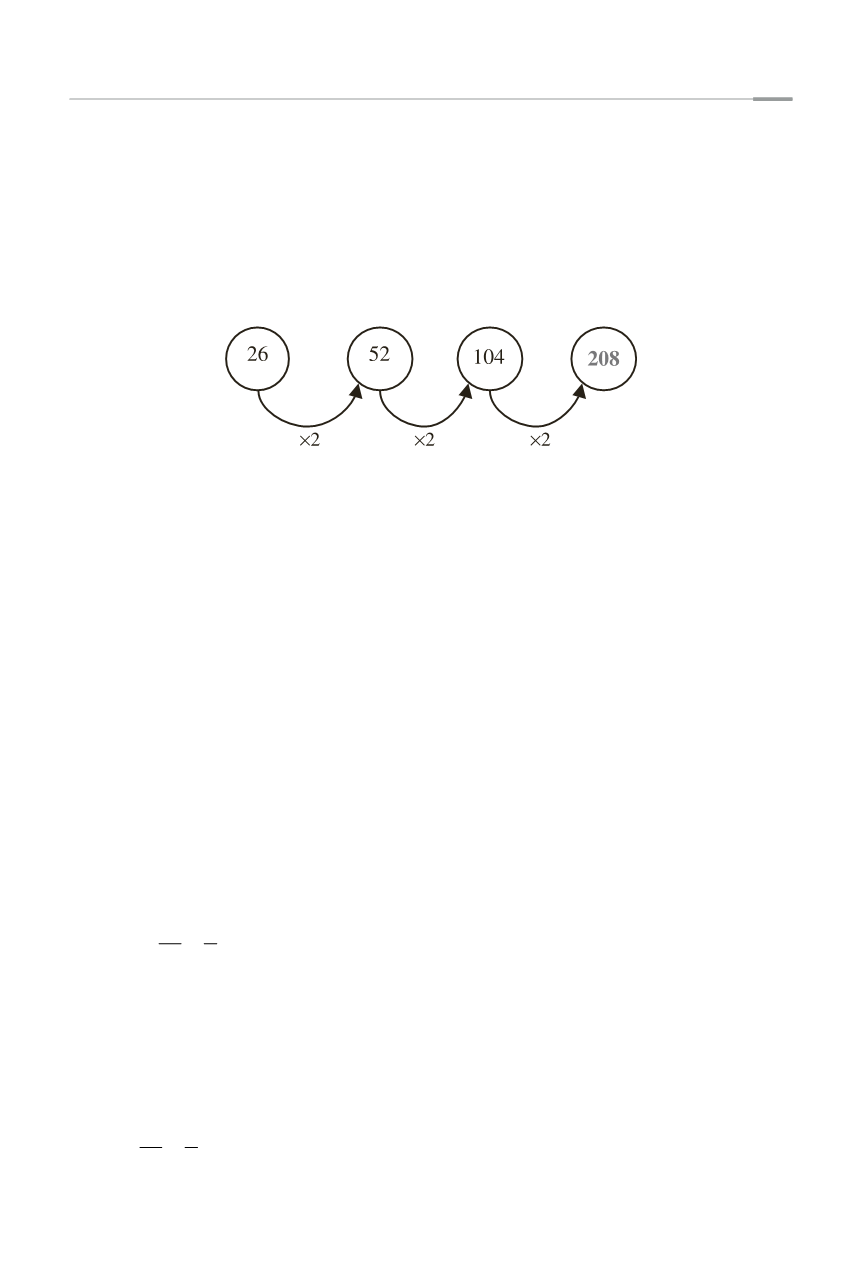
Ciascun numero è ottenuto moltiplicando il precedente per 2. In pratica ogni nu-
mero è il doppio del precedente. Difatti si ha:
26 × 2 = 52
52 × 2 = 104
Ed infine si ha:
104 × 2 = 208
Pertanto la risposta esatta è la D.
Di seguito si riporta uno schema che riassume il nesso logico della sequenza:
7)
B.
La prima equazione, trasportando a primo membro il termine ¿ e sommando,
diviene:
3¿ = #
Dovendo essere, in base alla terza equazione, ¿ = #, ne deriva che ¿ = # = 0.
La seconda equazione, sostituendo a ¿ e a ç i rispettivi valori, e cioè 0 e –6, diviene:
0 = –6 + $
da cui:
$ = 6
8)
D.
Si indica con
T
l’uscita di “testa” dal lancio di una moneta; analogamente si indica
con
C
l’uscita di “croce” dal lancio di una moneta.
Lanciando tre monete si possono ottenere otto possibili risultati:
TTT
,
TTC
,
TCC
,
CTT
,
CTC
,
CCT
,
CCC
,
TCT
.
Il numero di casi possibili, indicato con
n
p
, è dunque pari ad 8, ossia
n
p
= 8. Il caso fa-
vorevole è unico, ossia l’uscita della combinazione
TTT
(le tre teste). Pertanto il numero
di casi favorevoli, indicato con
n
f
, è pari a
n
f
= 1.
La probabilità che si verifichi una combinazione di tre teste, ossia
P
(
TTT
) è data dal
rapporto tra il numero di casi favorevoli e il numero di casi possibili. Pertanto si ha:
P TTT
n
n
f
p
(
)
= =
1
8
Quindi la risposta corretta è D.
Il quesito può essere risolto anche nel modo seguente.
Nel lancio della prima moneta vi sono due soli casi possibili, l’uscita di “testa” e
l’uscita di “croce”. Pertanto
n
p
= 2. Il caso favorevole, ossia l’uscita di “testa”, è unico.
Quindi
n
f
= 1. Pertanto la probabilità che esca testa nel lancio della prima moneta vale:
P T
n
n
f
p
1
1
2
( )
= =
















