
Parte Prima -
Nozioni teoriche
384
dispari si ottiene aggiungendo 1 alla cifra nella posizione dispari precedente; analoga-
mente, ciascuna cifra in posizione pari si ottiene dalla cifra precedente in posizione pari,
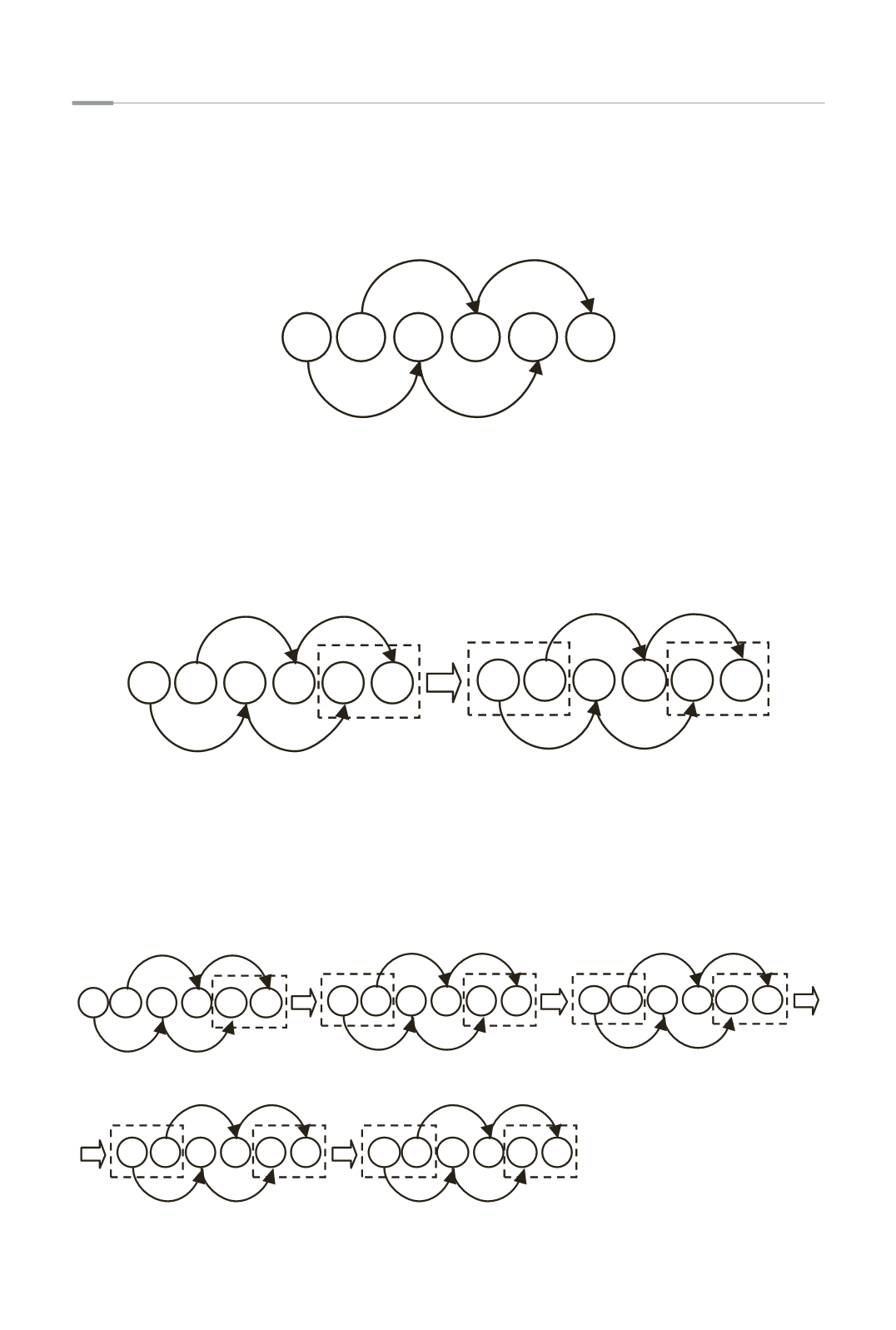
aggiungendo ad essa 1. Ad esempio per il primo gruppo di sei cifre, ossia 415263, si può
individuare il seguente nesso logico:
4
5
6
1
2
3
+1
+1
+1
+1
Ovviamente aggiungendo 1 alla cifra 9 si ottiene 10 a cui deve essere sostituita sempli-
cemente la cifra 0.
Terminato un gruppo di sei cifre, il gruppo successivo parte con l’ultima coppia di
cifre possedute dal gruppo precedente e procede sempre con il medesimo nesso logico.
Pertanto si ha:
4
5
6
1
2
3
+1
+1
+1
+1
6
7
8
3
4
5
+1
+1
+1
+1
In definitiva, proseguendo con tale legame logico si arriva a determinare l’ultimo
gruppo di sei cifre che deve partire con la coppia di cifre 29, presente alla fine del
gruppo precedente, e deve proseguire ottenendo ogni cifra in posizione pari dalla cifra
nella posizione pari precedente sommando ad essa 1 e facendo la medesima cosa con
le cifre in posizione dispari.
4
5
6
1
2
3
+1
+1
+1
+1
6
7
8
3
4
5
+1
+1
+1
+1
8
9
0
5
6
7
+1
+1
+1
+1
0
1
2
7
8
9
+1
+1
+1
+1
2
3
4
9
0
1
+1
+1
+1
+1
Pertanto l’ultimo gruppo di cifre è 293041 e la risposta corretta è A.
















